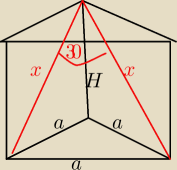
 Graniastosłup prawidłowy trójkątny => w podstawie trójkąt równoboczny
Pole trójkąta równobocznego:
Pp=a2√3/4=36√3
Stąd otrzymujemy, że a=12.
Spójrzmy teraz na trójkąt powstały z przekątnych ścian bocznych (czerwone odcinki) i podstawy
trójkąta.
Z twierdzenia cosinusów:
122=x2+x2−2x2cos30
144=2x2−2x2*√3/2
Rozwiązując dalej otrzymujemy:
x2=288+144√3
Teraz spójrzmy na trójkąt powstały z boków x,a,H− jest to trójkąt prostokątny, więc z
Pitagorasa:
H2+a2=x2
H2=x2−a2
H2=288+144√3−144
H2=144+144√3=144(1+√3)
H=12√1+√3
Mam nadzieję, że się nigdzie w rachunkach nie pomyliłam.
Graniastosłup prawidłowy trójkątny => w podstawie trójkąt równoboczny
Pole trójkąta równobocznego:
Pp=a2√3/4=36√3
Stąd otrzymujemy, że a=12.
Spójrzmy teraz na trójkąt powstały z przekątnych ścian bocznych (czerwone odcinki) i podstawy
trójkąta.
Z twierdzenia cosinusów:
122=x2+x2−2x2cos30
144=2x2−2x2*√3/2
Rozwiązując dalej otrzymujemy:
x2=288+144√3
Teraz spójrzmy na trójkąt powstały z boków x,a,H− jest to trójkąt prostokątny, więc z
Pitagorasa:
H2+a2=x2
H2=x2−a2
H2=288+144√3−144
H2=144+144√3=144(1+√3)
H=12√1+√3
Mam nadzieję, że się nigdzie w rachunkach nie pomyliłam. 
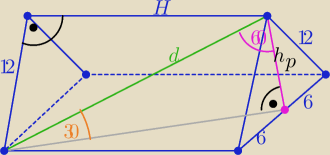 Pp=36√3 ⇒ a2√3}{4}=36√3 ⇒ a=12
Pp=36√3 ⇒ a2√3}{4}=36√3 ⇒ a=12
| a | ||
hp= | √3 = 6√3 | |
| 2 |