6 ponumerowanych kul chcemy rozmieścić losowo w 3ech szufladach. Oblicz prawdopo
Dramat..: Trójkąt prostokątny ABC jest opisany na okręgu. Punkt M styczności okręgu z przeciwprostokątną
AB podzielił przeciwprostokątną na odcinki długości 2a i 3a, gdzie a>0. Wykaż, że pole
trójkąta ABC jest równe 6a2
6 lut 17:21
5-latek:
Gdzie bedzie lezal punkt M?
6 lut 18:41
'Leszek: Przeciez to trojkat ma byc opisany na okregu , a nie odwrotnie !
6 lut 18:43
6 lut 19:35
'Leszek: Wykonaj rysunek dla trojkata prostokatnego w ktorym wpisany jest okrag.
Nastepnie skorzystaj z twierdzenia Pitagorasa
( 2a+ r)2 + (3a + r)2 = (2a+3a)2
otrzymasz r = a
Oraz przyprostokatne Δ , 3a i 4a
Pole PΔ = 0,5*3a*4a = 6a2
6 lut 20:17
Mila:
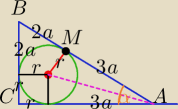
a>0 i r>0
(2a+r)
2+(3a+r)
2=(5a)
2⇔
r
2+5ar−6a
2=0
Δ=49a
2
| | −5a+7a | | −5a−7a | |
r= |
| =a lub r= |
| <0 |
| | 2 | | 2 | |
|BC|=2a+a=3a
|AC|=3a+a=4a
6 lut 20:20
Dramat..: Dziękuję.. Rysunek zrobiłam identyczny, że nie wpadłam na najzwyklejsze tw. Pitagorasa..
6 lut 21:43
5-latek: Oraz to ze odcinkki od dowolnego punktu lezacego na zewnatrz do punktow stycznosci sa rowne
Rowniez dziekuje .
6 lut 22:27
Mila:
6 lut 22:51
Eta:
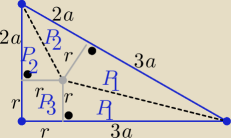2 sposób
2P=(2a+r)(3a+r)= 6a
2+5ar+r
2
i P=P
3+2P
1+2P
2=r
2+3ar+2ar= 5ar+r
2
to 2P=6a
2+P ⇒ P=6a
2
7 lut 02:19
Dramat..: Akurat na te długości odcinków wpadłam
no cóż, dziękuję raz jeszcze.
7 lut 08:37