wielomiany
maturzystkam: rowziąż nieróność:
Ix2−2xI≥x3
6 lut 00:00
maturzystkam: Rozwiąż nierówność*
6 lut 00:00
maturzystkam: nikt nic?

6 lut 00:16
Eta:
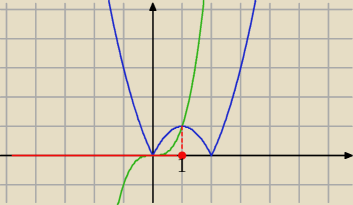
6 lut 00:17
maturzystkam: czyli trzeba to rozwiązać graficznie ?
6 lut 00:21
Adamm: możesz przedziałami jak wolisz
6 lut 00:22
maturzystkam:
właśnie cały czas próbuje przedziałami i mi nie wychodzi mam tak
Ix
2−2xI≥x
3
Ix
2−2xI−x
3≥0
x
2−2x=0 ⇒ x=0 i x=2
1) x∊(−
∞;0)
2) x∊<0;2)
3) x∊<2;=
∞)
dobre przedziały ?
6 lut 00:27
Janek191:
Tak

x
2 − 2 x = 0
x*( x − 2) = 0
Przedziały:
x ∊ ( −
∞, 0)
x ∊ < 0, 2)
x ∊ < 2, +
∞)
1) I x
2 − 2 x I = I x*( x − 2) I = x
2 − 2 x
x
2 − 2 x ≤ x
3
2)
I x
2 −2 x I = x*( x − 2) I = − x
2 + 2 x
− x
2 + 2 x ≥ x
3
3)
I x
2 − 2 x I = x
2 − 2 x
x
2 − 2 x ≥ x
3
6 lut 07:53
maturzystkam: czemu w pierwszym znak nierówności jest ≤ ?
6 lut 14:02
Alky: Powinno być ≥. Pomyłka
6 lut 14:12
maturzystkam: dobrze
6 lut 14:15
maturzystkam:
1)
x∊∊(−∞;0)
x2−2x≥x3
−x3+x2−2x≥0
x(−x2+x−2)≥0
x=0 Δ<0 ⇒ x∊(−∞;0)
2)
x∊<0;2)
−x2+2x≥x3
−x2−x2+2x≥0
(−x2−2x)(x−1)≥0
x=0 x=−2 x=1 ⇒ x∊<0;1)
3)
x∊<2;+∞)
x2−2x≥x3
−x3+x2−2x≥0
x(−x2+x−2)≥0
x=0 Δ<0 ⇒ x∊∅
wspólna część: x∊(−∞;1)
6 lut 14:31
maturzystkam: sprawdzi ktoś ?

6 lut 14:32


 właśnie cały czas próbuje przedziałami i mi nie wychodzi mam tak
Ix2−2xI≥x3
Ix2−2xI−x3≥0
x2−2x=0 ⇒ x=0 i x=2
1) x∊(−∞;0)
2) x∊<0;2)
3) x∊<2;=∞)
dobre przedziały ?
właśnie cały czas próbuje przedziałami i mi nie wychodzi mam tak
Ix2−2xI≥x3
Ix2−2xI−x3≥0
x2−2x=0 ⇒ x=0 i x=2
1) x∊(−∞;0)
2) x∊<0;2)
3) x∊<2;=∞)
dobre przedziały ?
 x2 − 2 x = 0
x*( x − 2) = 0
Przedziały:
x ∊ ( −∞, 0)
x ∊ < 0, 2)
x ∊ < 2, +∞)
1) I x2 − 2 x I = I x*( x − 2) I = x2 − 2 x
x2 − 2 x ≤ x3
2)
I x2 −2 x I = x*( x − 2) I = − x2 + 2 x
− x2 + 2 x ≥ x3
3)
I x2 − 2 x I = x2 − 2 x
x2 − 2 x ≥ x3
x2 − 2 x = 0
x*( x − 2) = 0
Przedziały:
x ∊ ( −∞, 0)
x ∊ < 0, 2)
x ∊ < 2, +∞)
1) I x2 − 2 x I = I x*( x − 2) I = x2 − 2 x
x2 − 2 x ≤ x3
2)
I x2 −2 x I = x*( x − 2) I = − x2 + 2 x
− x2 + 2 x ≥ x3
3)
I x2 − 2 x I = x2 − 2 x
x2 − 2 x ≥ x3
