W trójkącie ABC środkowe AK i CL są do siebie prostopadłe. Oblicz pole trójkata
SEKS INSTRUKTOR :
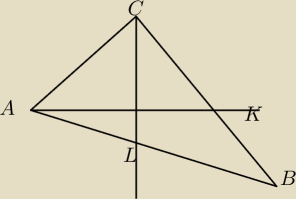
W trójkącie ABC środkowe AK i CL są do siebie prostopadłe. Oblicz pole trójkata ABC wiedząc, że
|AK|=10 i |CL|=8
Proszę o pomoc
5 lut 20:34
5-latek:
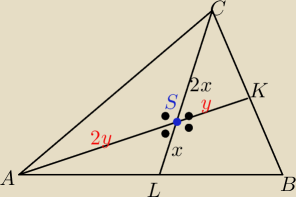
Punkt S dzieli srodkowe w stosunku 2:1 liczac od wierzcholka trojkata
5 lut 20:46
SEKS INSTRUKTOR : no i to to wiem, ale co z tym dalej?
wszystko fajnie , bo pola ACS , ALS i SCK policze, a co z polem SKBL ?
5 lut 20:49
5-latek: Skoro wiedziales to dlaczego nie napisales?
5 lut 20:51
5-latek: Przeciez znasz dlugosci wszystkich jego bokow
5 lut 20:55
SEKS INSTRUKTOR : zrobiłem tyle co Ty i dalej nie wiem jak sie ruszyc, pokombinuje :C
5 lut 20:59
5-latek: Mowie tutaj o trojkacie ABC .
5 lut 20:59
5-latek: AB=2AL i AL z Pitagorasa
AC z Pitagorasa
Cb= 2*CK i Ck z Pitagorasa
Pole z Herona
ja bym tak robil
Moze jest inny sposob
5 lut 21:01
SEKS INSTRUKTOR : no i nadal nie wiem co z SKBL
5 lut 21:04
SEKS INSTRUKTOR : dzikie to wychodzi, nie mam siły do tego bajzlu
5 lut 21:09
Mila:
I co to za zwątpienie?
5 lut 21:11
5-latek:
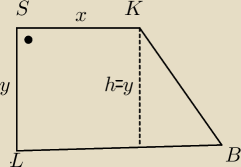
A po co CI czworokat SKBL
Do Herona potrzene sa 3 boki
Ale skoro uparles sie na ten czworokat to zauwaz z eto bezie trapez prostokatny
KB= CK i LB=AL
5 lut 21:11
5-latek: Popraw na rysunku (bo wpisalem x i y odwrotnie
Wtedy h=x
5 lut 21:13
Mila:
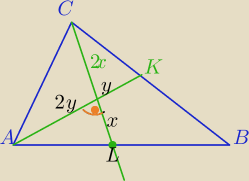
3x=8
P=P
ΔABC
| | 1 | | 1 | | 80 | | 80 | |
PΔAKC= |
| *2y*2x+ |
| *y*2x=3xy=3* |
| = |
| |
| | 2 | | 2 | | 9 | | 3 | |
5 lut 21:23
Bogdan:
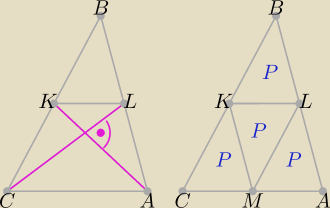
Moja propozycja.
| | 1 | |
Szkic. |AK| = 10, |CL| = 8, Pole PCALK = |
| * 10 * 8 = 40 |
| | 2 | |
Trójkąty CMK, MAL, MLK i KLB są przystające, pole każdego z nich jest równe P.
Pole trójkąta ABC jest równe P{ABC} = 4P, pole czworokąta CALK jest rowne 3P = 40,
| | 40 | | 160 | |
stąd 4P = 4* |
| = |
| |
| | 3 | | 3 | |
5 lut 21:37
SEKS INSTRUKTOR :
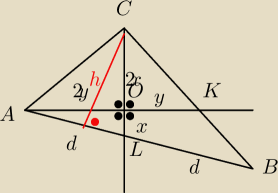
Zrobilem jeszcze inaczej
x=8/3
y=10/3
P
AOC = 1/2*2x*2y=160/3
P
ALO=1/2*2y*x=90/3
Suma tych trójkatów daje pole trójkąta ALC
Trójkąt ALC ma podstawę długości d i wysokość h, tak samo jak trójkąt BLC, czyli trójkaty te
mają takie same pola.
Pole ABC = 2* P
ALC = 2*(240/3) = 160
5 lut 21:40
Mila:
Sposób dobry, ale masz błędy rachunkowe.
5 lut 21:59
Eta:
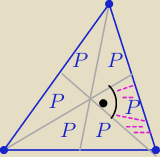
Moja propozycja
 Trzy środkowe dzielą trójkąt na 6 trójkątów o równych polach
i dzielą się w stosunku 2:1 licząc od wierzchołka
Trzy środkowe dzielą trójkąt na 6 trójkątów o równych polach
i dzielą się w stosunku 2:1 licząc od wierzchołka
Uwzględniając dane w treści zadania:
| | 8 | | 20 | | 160 | |
P(ABC)=6*P= 3* |
| * |
| = |
| [j2] |
| | 3 | | 3 | | 3 | |
5 lut 23:16
 W trójkącie ABC środkowe AK i CL są do siebie prostopadłe. Oblicz pole trójkata ABC wiedząc, że
|AK|=10 i |CL|=8
Proszę o pomoc
W trójkącie ABC środkowe AK i CL są do siebie prostopadłe. Oblicz pole trójkata ABC wiedząc, że
|AK|=10 i |CL|=8
Proszę o pomoc
 Punkt S dzieli srodkowe w stosunku 2:1 liczac od wierzcholka trojkata
Punkt S dzieli srodkowe w stosunku 2:1 liczac od wierzcholka trojkata
 A po co CI czworokat SKBL
Do Herona potrzene sa 3 boki
Ale skoro uparles sie na ten czworokat to zauwaz z eto bezie trapez prostokatny
KB= CK i LB=AL
A po co CI czworokat SKBL
Do Herona potrzene sa 3 boki
Ale skoro uparles sie na ten czworokat to zauwaz z eto bezie trapez prostokatny
KB= CK i LB=AL
 3x=8
3x=8
 Moja propozycja.
Moja propozycja.
 Zrobilem jeszcze inaczej
x=8/3
y=10/3
PAOC = 1/2*2x*2y=160/3
PALO=1/2*2y*x=90/3
Suma tych trójkatów daje pole trójkąta ALC
Trójkąt ALC ma podstawę długości d i wysokość h, tak samo jak trójkąt BLC, czyli trójkaty te
mają takie same pola.
Pole ABC = 2* PALC = 2*(240/3) = 160
Zrobilem jeszcze inaczej
x=8/3
y=10/3
PAOC = 1/2*2x*2y=160/3
PALO=1/2*2y*x=90/3
Suma tych trójkatów daje pole trójkąta ALC
Trójkąt ALC ma podstawę długości d i wysokość h, tak samo jak trójkąt BLC, czyli trójkaty te
mają takie same pola.
Pole ABC = 2* PALC = 2*(240/3) = 160
 Moja propozycja
Moja propozycja Trzy środkowe dzielą trójkąt na 6 trójkątów o równych polach
i dzielą się w stosunku 2:1 licząc od wierzchołka
Uwzględniając dane w treści zadania:
Trzy środkowe dzielą trójkąt na 6 trójkątów o równych polach
i dzielą się w stosunku 2:1 licząc od wierzchołka
Uwzględniając dane w treści zadania: