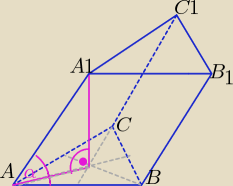
 Podstawami graniastosłupa pochyłego są trójkąty równoboczne ABC i A1B1C1 o boku a. Rzytem
prostokątnym wierzchołka A1 jest środek ciężkości drugiej podstawy a krawędź AA1 tworzy z
krawędzią podstawy kąt α=π4. Wyznacz objętość i Pole powierzchni bocznej.
Podstawami graniastosłupa pochyłego są trójkąty równoboczne ABC i A1B1C1 o boku a. Rzytem
prostokątnym wierzchołka A1 jest środek ciężkości drugiej podstawy a krawędź AA1 tworzy z
krawędzią podstawy kąt α=π4. Wyznacz objętość i Pole powierzchni bocznej.
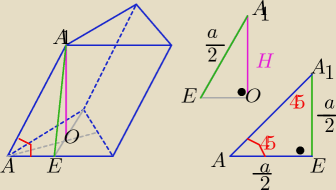 zobacz na rys.
zobacz na rys.
| a√3 | ||
IOEI= | ||
| 6 |
| a | ||
IIAEI=IA1EI= | ......bo ΔAEA1 jest prostokątny i równoramienny
| |
| 2 |
| a2 | a2 | a2 | ||||
H2 = IEA1I2 − IEOI2 = | − | = | ||||
| 4 | 12 | 6 |
| a√6 | ||
więc H= | ||
| 6 |
| a2√3 | ||
to V= | *H=......... dokończ
| |
| 4 |
| a3√2 | ||
odp: V= | [j3]
| |
| 8 |
| a | 3a2 | |||
Pb= 3a*h(ściany)= 3a* | = | [j2] | ||
| 2 | 2 |



 Bo wiem dlaczego jest prostokątny
Bo wiem dlaczego jest prostokątny