pochodna dawidos345: Wyznacz przedziały monotoniczności funkcji f(x)=(5+3x²)/(4+x² ). pochodna wychodzi f'(x)=14x/(4+x²)² a w odpdp. f maleje w przedziałach: 〈−1,0),(0, 1〉, f rośnie w przedziałach: (−∞ 1〉,〈1,+∞)

Jerzy:

	6x(4+x2) − 2x(5+3x2)
f'(x) =
	(4+x2)2

dawidos345: co dalej?

Janek191:

dawidos345: mozna jaśniej ?

Jerzy: Masz błąd w odpowidzi.

dawidos345: dobra dziękuje

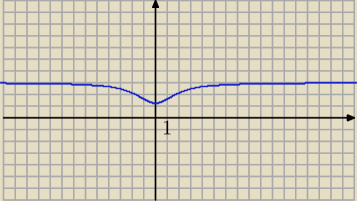
Janek191: Pewnie odpowiedź jest od innego zadania

Jerzy:

	14x
f'(x) =
	(x2+4)2

Zatem funkcja maleje dla x ∊ (−∞;0) i rośnie dla x ∊ ( 0;+∞)