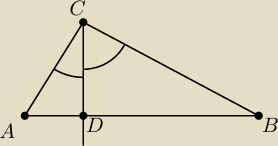
W trójkącie ABC z wierzchołka kąta prostego poprowadzono prostą Gymbus: Jak na rysunku, oraz: ∡ACD = 30st ∡DCB = 60st |DB| = 2|AD| Wiedząc, że |AC| = √3 oblicz długości pozostałych boków tego trójkąta. Uwaga! Przy wierzchołku D nie ma kątów prostych.

Gymbus: Pomóżcie proszę

Janek191: I AC I = √3 ⇒ I AD I = 0,5√3 I DB I = 2 I AD I = √3 więc I AB I = 0,5 √3 + √3 = 1,5 √3 Z tw. Pitagorasa I BC I² = I AB I² − I AC I² = 2,25*3 − 3 = 3,75

	√15
I BC I = √ 3,75 =		= 0,5 √15
	2

Pytający: @Janek191 Uwaga! Przy wierzchołku D nie ma kątów prostych.

Pytający: |AB|=3|AD| |BC|=√9|AD|²−3 P_ABC=P_ACD+P_BCD

1		1		1
	√3|BC|=		√3|CD|sin30o+		|BC||CD|sin60o
2		2		2

	2|BC|		2√9|AD|2−3
|CD|=		=
	1+|BC|		1+√9|AD|2−3

twierdzenie cosinusów: |AD|² = |AC|²+|CD|²−2|AC||CD|cos30^o |AC| podane, podstawiasz |CD| i liczysz |AD| mając |AD| policzysz już boki brzmi prosto, ale w ten sposób wychodzi takie piękne równanie (x=|AD|): https://www.wolframalpha.com/input/?i=x%5E2%3D3%2B((2sqrt(9x%5E2-3))%2F(1%2Bsqrt(9x%5E2-3)))%5E2-2sqrt(3)(2sqrt(9x%5E2-3))%2F(1%2Bsqrt(9x%5E2-3))cos(pi%2F6) rozwiązanie to:

	√7
|AD|=
	3

tym samym |AB|=√7, |BC|=2 nie mam pojęcia, czy łatwo tamto równanie uprościć, ale obliczyć jak widać się da...

Gymbus: @Mila To samo: |CD| to nie wysokość. Sorry za sugestię, ale rysunek w zadaniu mam taki sam, to stwierdziłem, że w razie gdyby polecenie miało się okazać lewe zostawię go bez zmian. Właśnie wpadłem na rozwiązanie i wychodzi prawidłowe, gdyby ktoś chciał wiedzieć: 1. z tw. cos |CD| w zależności od |AD| 2. z pitagorasa |CB| w zależności od |AD| 3. z tw. cos |AD| w trójkącie ACD lub CDB

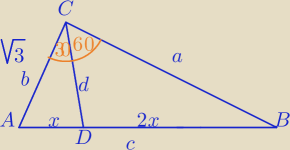
Mila: b=√3 P_ΔCDB=2*P_ΔCDA⇔

1		1
	*d*a*sin60o=2*		*√3*d*sin30o
2		2

	√3		1
a*		=2*√3*
	2		2

a=2 c²=2²+(√3)² c²=7 c=√7 =====

Mila: Zmyliłeś mnie tym nickiem i nie przeczytała dokładnie zadania.

Eta: A już miałam to samo pisać

Mila: Hej Eto

Mila: