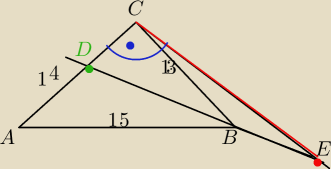
Trojkat i dwusieczna 5-latek: W trojkacie ABC dane sa boki AB=15 AC= 14 i CB=13 Dwusieczna kąta B przedluzono poza wierzcholek tego kąta do przeciecia sie w punkcie E z prostopadla do AC wyprowadzona z wierzcholka C Obliczyc CE Trojkat CDE jest trojkatem prostokatnym Z tw o dwusiecznej wylicze dlugosc odcinka CD CD=x AD= 14−x

13		15
	=
x		14−x

x= 6,5 Teraz jabbym mial dugosc odcinka DE to byloby po zadaniu

5-latek:

5-latek: Zostawiam to zadanie Muszse porobic troche zadan z podobienstwem trojkatow zeby widziec trojkaty podobne Tutaj jednak jest wskazowka do tego zadania zeby poprawdzic wysokosc trojkata ABC i skorzystac z podobienstwa trojkatow

5-latek: Jak mam tutaj skorzystac z tego podobienstwa ? jednak chce skonczyc to zadanie

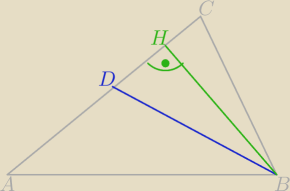
Rafal: O ile się nie mylę, to trójkąty HDB i CDE są podobne. Najpierw możemy policzyć długość wysokości, potem długość odcinka HC, potem długość odcinka HD, potem długość dwusiecznej BD itd.

Rafal:

	HB		HB
Aha, punkt H leży pomiędzy punktami D i C, gdyż cos(HBC)=		>		=cos(HBA), a
	13		15

	π
ponieważ funkcja y=cos(x) w przedziale (0,		) jest malejąca, to kąt HBC ma miarę
	2

mniejszą od kąta HBA.

Mila: Jaka jest odpowiedź?

5-latek: Dobry wieczor Milu odpowiedz do zadania to CE=52. Walcze teraz Milu z piecem bo cofa mi dym z pieca a mam go w kuchni .

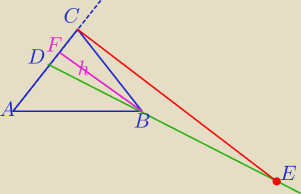
Mila: |DC|=6.5 P_ΔABC=√21*(21−15)*(21−14)*(21−13)=84

1
	*14*h=84
2

h=12 |FC|²+h²=13² |FC|=5, |FD|=1.5

	DC		6.5		13
ΔDCE∼ΔDFB w skali k=		=		=
	DF		1.5		3

CE		13
	=
h		3

	13
|CE|=		*12=52
	3

=============

5-latek: dziekuje CI bardzo Na razie jesczcze nie bardzo widze te trojkaty podobne i jka je liczyc Zrobie sobie potem dwa zadania ze zbioru Malem M (z tych trojkatow

5-latek: A te trojkaty sa podobne wedlug cech BKB?

5-latek:

Mila: Są prostokątne i kąt CDB wspólny.

5-latek: Dobrze