trapez kontik: Jeszcze jedno zadanie z trapezem W trapezie równoramiennym ABCD (AB∥CD) opisanym na okręgu |AB|=3|CD| oraz punkty E i F są punktami styczności okręgu odpowiednio z bokami AB i AD. Odcinek EF przecina przekątną AC tego trapezu w punkcie M

	|ME|
Wykaż,że		=2
	|MF|

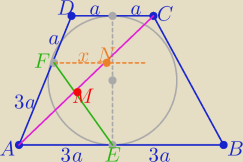Eta: Prowadzimy prostą FN ∥AB 1/ z podobieństwa trójkątów ADC i ANF z cechy (kkk)

	2a		4a		3
		=		⇒ x=
	x		3a		2

2/ i ponownie z podobieństwa trójkątów AME i FMN z cechy (kkk)

	|ME|		3a
		=		⇒ ...... teza
	|MF|		x

Janek191:

	3
x =		a
	2

I ME I		3a
	=		= 2 ckd.
I MF I		1,5a

Eta:

	3
Chochlik ... x=		a
	2