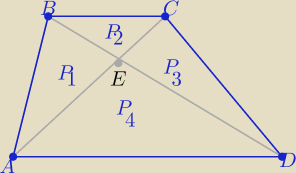
trapez kontik: W czworokącie wypukłym ABCD przekątne AC i BD przecinają się w punkcie E pola trójkątów : P₁=[ABE]. P₂=[BCE], P₃=[CDF], P₄=[DAE]

	P1+P3
Wiedząc,że		=√P2P4 ( pod pierwiastkiem jest P1*P2
	2

Wykaż,że czworokąt ABCD jest trapezem

Janek191: To w końcu pod znakiem √ jest P₂*P₄ , czy P₁*P₂ ?

kontik: jest P₂*P₄

5-latek: czesc Janek191 Moze chodzi o taki zapis

P1+P3
	= U{√P2*P4{P1*P2}
2

Eta: Można tak: W drugą stronę Jeżeli czworokąt ABCD jest trapezem to: P(trapezu)=(√P4+√P₂)² P₁+P₂+P₃+P₄=P₂+P₄+2√P₂*P₄

	P1+P3
P1+P3 =2√P2*P4 ⇒		=√P2*P4 −− zgodne z założeniem
	2