geometria analityczna Krzecho: Załóżmy , że mamy trójkąt a na nim opisany okrąg i środek okręgu jest w jednym z jego wierzchołków to czy jest to jakiś szczególny przypadek trójkąta

Jerzy: To jest niemożliwe. Jak środek okręgu opisanego może być wierzchołkiem trójkąta ?

Krzecho:

	5		7
no dobra może ja źle zinterpretowałem.. taka jest treść zadania.Punkt P=(		,−		) jest
	2		2

środkiem podstawy AB trójkąta ABC, którego wierzchołki A,B należą do okręgu o równaniu x²−4x+y²=21. i tutaj "Punkt C pokrywa się ze środkiem okręgu". Wyznacz wierzchołki A,B i pole trójkąta ABC

Jerzy: Przecież to brednie ... wierzchołki trójkąta muszą należeć do okręgu, a więc punkt C też należy do okręgu, zatem nie może "pokrywać się ze środkiem okręgu"

5-latek: Dzien dobry Jerzy Kolego srodekm okregu opisanego na trojkacie lezy a) wewnatrz trojkata gdy trojkat jest ostrokatny b) na srodku przeciwprostokatnej w trojkacie prostokatnym c) na zewnatrz trojakta gdy trojkat jest rozwartokatny .

Jerzy: Witaj

human: ? więc jak wyznaczyć podstawę

iteRacj@: "no dobra może ja źle zinterpretowałem.." źle, bo w treści zadania nigdzie nie jest powiedziane, że okrąg jest opisany na trójkącie jedynie: wierzchołki A,B należą do okręgu i wierzchołek C pokrywa się ze środkiem okręgu

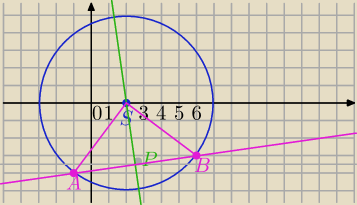
Mila: x²−4x+y²=21⇔(x−2)²+y²=25 S=(2,0) r=5 1) równanie prostej PS 0=2a+b

	7		5
−		=		a+b
	2		2

========= a=−7, b=14 y=−7x+14 2) P jest środkiem cięciwy AB⇔SP⊥AB

	1
c: y=		x+b i P∊c
	7

	7		1		5		7		5
−		=		*		+b⇔b=−		−
	2		7		2		2		14

	27
b=−
	7

3) cięciwa AB zawiera się w prostej:

	1		27
c: y=		x−		/*7
	7		7

7y=x−27 x=7y+27 4) podstawiamy do równania okręgu: (x−2)²+y²=25 (7y+27−2)²+y²=25 (7y+25)²+y²=25 stąd: y=−4 lub y=−3 x=7*(−4)+27=−1⇔ A=(−1,−4) lub x=7*(−3)+27=6⇔ B=(6,−3) 5) oblicz pole ΔABC