calki oznaczone Jack: Całki oznaczone dylemat obliczyc pole ograniczone krzywymi x²+y² = 16 x²=12y−12 gdy sprowadze to do igreka i podstawie do wzoru to wychodzi troche skomplikowana calka i sporo liczenia, wiec moje pytanie czy da sie prosciej. Bo chyba nie moge dac x² do calek? wtedy bym mial 2 ∫ [(16−y²) − 12y + 12] −14 Ale to raczej jest bledne. jak to moge zrobic w miare prosto?

Saizou : aaa... współrzędne biegunowe ?

ByłemLegendą: Nie lepiej jest znaleźć punkty przecięcia (2√3 i −2√3) rozdzielić sobie x²+y² = 16 na y=√16−x² i y=−√16−x² i policzyć całkę oznaczoną:

	1
2*∫02√3 [√16−x2 −		x2−1]dx ?
	12

Jack: no wlasnie calka √16−x² jest delikatnie nie przyjemna. Oczywiscie do policzenia ale szukam najprostszego sposobu Co do wspolrzednych biegunowych, co masz na mysli ?

Jack: ref

jc: Tniesz okrąg parabolą. Który fragment wybierasz, ten powyżej paraboli, czy ten poniżej? Znasz wzór na pole wycinak koła. Połącz fakty i będziesz miał wynik.

Mariusz: Jack co nie miałeś jeszcze całkowania przez części , a zabierasz się za równania różniczkowe nieźle

	x(−x)
∫√16−x2dx=x√16−x2−∫		dx
	√16−x2

	16−x2+16
∫√16−x2dx=x√16−x2−∫		dx
	√16−x2

	dx
∫√16−x2dx=x√16−x2−∫√16−x2dx+16∫
	√16−x2

	x
2∫√16−x2dx=x√16−x2+16arcsin(		)+C1
	4

	1		x
∫√16−x2dx=		(x√16−x2+16arcsin(		))+C
	2		4

Mariusz: W drugiej linijce w liczniku powinno być 16−x²−16

Jack: Oczywiscie mialen calkowanie przez czesci. @jc wybieram fragment "wewnatrz" paraboli. @Mariusz Ja wiem jak policzyc ten pierwiastek. Co wiecej licze dokladnir tym sposobem co Ty. Jednakze szukam jakiegos sposobu zeby nie wchodzic w calke z tym pierwiastkiem.

Mariusz: Wg mnie to jest najłatwiejszy sposób Podstawienie Eulera dałoby taką całkę ∫√16−x²dx √16−x²=(4−x)t (4−x)(4+x)=(4−x)²t² 4+x=(4−x)t² 4+x=4t²−xt² x+xt²=4t²−4 x(t²+1)=4t²−4

	4t2−4		4t2+4−8		8
x=		=		=4−
	t2+1		t2+1		t2+1

	8t
(4−x)t=
	t2+1

dx=(−8)(−1)(t²+1)⁻² 2tdt

	16t
dx=		dt
	(t2+1)2

	8t	16t
∫			dt
	t2+1	(t2+1)2

	t2
=128∫		dt
	(t2+1)3

Są jeszcze współczynniki nieoznaczone Przewidujesz postać funkcji pierwotnej i różniczkujesz obustronnie aby obliczyć współczynniki Możesz jeszcze podstawić funkcje cyklometryczne i bawić się funkcjami trygonometrycznymi

Jack: czyli pierwiastka nie unikniemy...

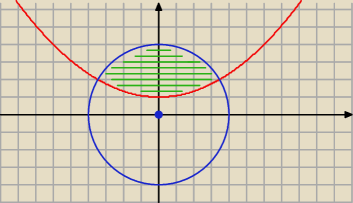
Jack: @jc jak tu wykorzystac wycinek kola?

jc: Połącz odcinkiem punkty przecięcia (−2√3,2), (2√3,2). Parabola poniżej tego odcinak ma pole 8/√3 (sprawdź!). Wycinek koła (−2√3,2), (0,0), (2√3,2) ma pole 16π/3. Część koła powyżej odcinka = wycinek koła − trójkąt = 16π/6 − 4√3 Szukane pole = 8/√3 − 4√3 + 16π/3 = 16π/3 − 4/√3. Sprawdź lepiej wszystkie rachunki.

Jack: ok, to mam z calki pliczyc jak rozumiem.

8
	sie zgadza.
√3

	α
Skad wiemy, jaki kat mamy w tym wycinku ? ze wzoru na		...
	360

mozna z pitagorasa ale...

	16π
ok, wlasciwie to bedzie 120 stopni... czyli		tez sie zgadza.
	3

	1		8√3
Pole trojkata =		* 16 * sin 120 =		= 4√3
	2		2

ok wychodzi ze sie zgadza. Super, dziekuje, az tak o tym nie myslalem