matematykaszkolna.pl
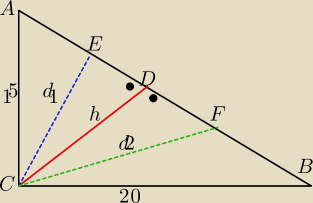
Trojkat prostokatny 5-latek: rysunekW trojkacie prostokatnym o przyprostokatnych 15 dcm i 2 m poprowadzono z wierzcholka kąta prostego wysokosc oraz dwusieczne obydwu kątow jakie wysokosc tworzy z rzyprostokatnymi . Obliczyc odcinek przeciwprostokatnk zawarty miedzy dwusiecznymi . Z zadania AB= √152+202= √625= 25 Obliczam h PABC= 05*300= 150 0,5*25*h= 150
 150 1500 300 60 
h=
=
=
=
=12
 12,5 125 25 5 
Obliczam AD AD= √152−122= √225−144= 9 BD= 25−9=16 I na tym moja inwencja tworcza sie na razie konczy
3 lut 20:21
Omikron: Twierdzenie o dwusiecznej emotka
3 lut 20:46
5-latek: czesc Nie wiem jak zastosowac
3 lut 20:48
Omikron:
|BF| |CB| 
=
|FD| |CD| 
|DE| |CD| 
=
|EA| |AC| 
3 lut 20:53
5-latek: Bo tak
h AC 
=
ed AE 
 BC h 
i drugie
=
 FB DF 
Nie znam dlugosci tych odcinkow w mianownikach
3 lut 20:53
Omikron: Ale znasz sumę długości tych odcinków. Oznacz jeden jako x, drugi jako ... −x
3 lut 20:55
5-latek: Za chwile wroce do tego Wybacz zle sie poczulem .
3 lut 20:57
Omikron: Nie ma sprawy, jak się kiepsko czujesz to odpocznij
3 lut 20:58
5-latek:
h AC 
=
ED AE 
AE=x ED=9−x
12 15 
=
9−x x 
z tego x=5 ED=4
BC h 
=
FB DF 
FB=p DF= 16−p
20 12 
=
p 16−p 
z tego p=10 DF= 16−10=6 ED+DF= 4+6=10 Zgadza sie z odpowiedza . Dzieki Omikron emotka
3 lut 22:12
Omikron: emotka
3 lut 22:16