Geometria analityczna Crash: Dane są wierzchołki A(−4,2) B(8,−2) C(6,4) trapezu równoramiennego ABCD o podstawie AB . Oblicz współrzędne wierzchołka D. Próbowałem policzyć z własności że przekątne mają taką samą długość, ale jakoś nie może mi wyjść poprawny wynik. Proszę o pomoc

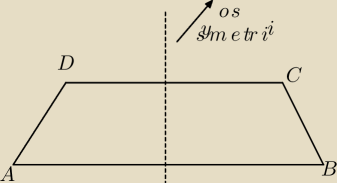
5-latek: I to powinno juz wszystko wyjasnic

Crash: Muszę się przyznać, że niezbyt mi to pomaga

5-latek: Napisz rownanie prostej rownoleglej do AB i przechodzacej przez punkt C TRapez ma os symetrii wiec rownanie symetralej AB trzeba napisac Dostajesz punkt S (przeciecia tych prostych Teraz Pubkt D jest rowno oddalony od C (ze wzoru na srodek odcinka wylicz wspolrzedne punktu D

5-latek: Poprawian Odlegosc punktu D od S jest taka sama jak punktu C od S

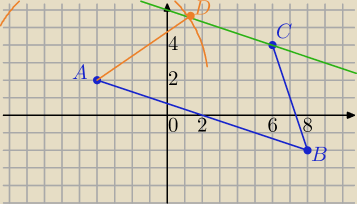
Mila: Wierzchołki A(−4,2), B(8,−2) C(6,4) 1) Prosta AB: y=ax+b wyznaczymy a 2=a*(−4)+b −2=a*8+b

	1
−−−−−−−−−− ⇔a=−
	3

	1
AB: y=−		x+b
	3

CD||AB⇔ 2) Prosta CD ma taki sam wsp. kierunkowy

	1		1
y=−		x+b i przechodzi przez punkt C⇔4=−		*6+b
	3		3

b=6

	1
Prosta CD: y=−		x+6
	3

3) |BC|=|AD|=√2²+6²=√40 4) geometrycznie D wyznaczymy kreśląc okrąg o środku D i r=√40 Równanie okręgu: (x+4)²+(y−2)²=40 i prosta CD

	1
y=−		x+6 stąd x=−3y+18
	3

(−3y+18+4)²+(y−2)²=40 po rozwiązaniu:

	28
y=		lub y=8
	5

podstawiamy do równania prostej CD

	28		6
x=−3*		+18=		lub x=6
	5		5

	6		28
D=(		,		) lub D=(6,8) ( to będzie równoległobok)
	5		5

5-latek: Dobry wieczor Milu

Mila: Witaj, już zdrowy?

5-latek: Milu Juz prawie . Jeszcze bylem dzisiaj u Pani doktor , osluchala mnie i stweirdzila ze dobrze ale jeszcze dala zwolnienie do poniedzialu Jeszcze jestem troche oslabiony (mam jescze odpoczac.

Mila: No to zdrowiej ładnie W Krakowie smog , nie wychodzimy nigdzie. Może jutro będzie lepiej.

5-latek: To niedobrze Milu Mozna sie od tego smogu powaznie rozchorowac U ,mnie na wsi tez pala czym popadnie nawet plastikami