| ⎧ | x2e−x{2} gdy x≤1 | ||
| f(x) = | ⎨ | ||
| ⎩ | 1/e + Ax2 gdy x>1 |
| f(1−Δx) −f(1) | ||
lim Δx→0− | ||
| Δx |
| (1−Δx)2*e−(1−Δx) −12e−1 | ||
lim Δx→0− | ||
| Δx |
| e−1 −1 | ||
po dalszych przeksztalceniach i podstawieniu 0 dochodze do postaci lim Δx→0− | ||
| 0 |
 moglby ktos wytlumaczyc?
moglby ktos wytlumaczyc?
 A = 0
II wersja
A = 0
II wersja 
| 1 | ||
f(x) = | + Ax2 dla x > |1| | |
| e |

 Funkcja f(x) jest różniczkowalna na ℛ\{−1,1} jako złożenie funkcji elementarnych.
pochodna lewostronna w −1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E-+of+(1%2Fe%2Bb(-1%2Bh)%5E2-1%2Fe-b(-1)%5E2)%2Fh
limx→−1− f(x) = −2A
pochodna prawostronna w −1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E%2B+of+((-1%2Bh)%5E2e%5E(-(-1%2Bh)%5E2)-(-1)%5E2e%5E(-(-1)%5E2))%2Fh
limx→−1+ f(x) = 0
pochodna lewostronna w 1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E-+of+((1%2Bh)%5E2e%5E(-(1%2Bh)%5E2)-1%5E2e%5E(-(1)%5E2))%2Fh
limx→1− f(x) = 0
pochodna prawostronna w 1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E%2B+of+(1%2Fe%2Bb(1%2Bh)%5E2-1%2Fe-b*1%5E2)%2Fh
limx→1+ f(x) = 2A
Aby f(x) była różniczkowalna w −1 i 1 musi mieć w tych punktach skończone pochodne, więc:
−2A=0 ∧ 0=2A ⇒ A=0
Poza tym jeśli rozważysz:
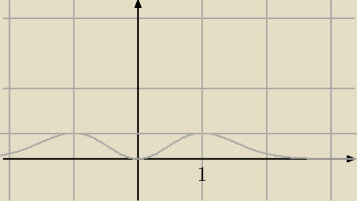
g(x)=x2e−x2, x∊ℛ
Funkcja f(x) jest różniczkowalna na ℛ\{−1,1} jako złożenie funkcji elementarnych.
pochodna lewostronna w −1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E-+of+(1%2Fe%2Bb(-1%2Bh)%5E2-1%2Fe-b(-1)%5E2)%2Fh
limx→−1− f(x) = −2A
pochodna prawostronna w −1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E%2B+of+((-1%2Bh)%5E2e%5E(-(-1%2Bh)%5E2)-(-1)%5E2e%5E(-(-1)%5E2))%2Fh
limx→−1+ f(x) = 0
pochodna lewostronna w 1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E-+of+((1%2Bh)%5E2e%5E(-(1%2Bh)%5E2)-1%5E2e%5E(-(1)%5E2))%2Fh
limx→1− f(x) = 0
pochodna prawostronna w 1: https://www.wolframalpha.com/input/?i=limit+as+h-%3E0%5E%2B+of+(1%2Fe%2Bb(1%2Bh)%5E2-1%2Fe-b*1%5E2)%2Fh
limx→1+ f(x) = 2A
Aby f(x) była różniczkowalna w −1 i 1 musi mieć w tych punktach skończone pochodne, więc:
−2A=0 ∧ 0=2A ⇒ A=0
Poza tym jeśli rozważysz:
g(x)=x2e−x2, x∊ℛ
| 1 | ||
h(x)= | +Ax2, x∊ℛ | |
| e |
| f(a+h)−f(a) | f(a+h)−f(a) | |||
limh−>0− | = limh−>0+ | = g ∧ g∊(−∞,∞) | ||
| h | h |