ostrosłup janek: Podstawą ostrosłupa jest trapez równoramienny, którego kąt ostry ma miarę 60° i który opisany jest na okręgu o promieniu r=10. Każda ściana boczna ostrosłupa tworzy z płaszczyzną postawy kąt o mierze równej 45°. Oblicz objętość ostrosłupa. Oznaczyłem wierzchołek ostrosłupa jako S. Środek okręgu jako O. K jako promień rzutowany na jeden z boków. I wyszło mi tak:

SO
	= tg45°, czyli SO = 10. No i niby mam wszystko, ale jak obliczyć pole podstawy bez
KO

boków? Dzięki za pomoc.

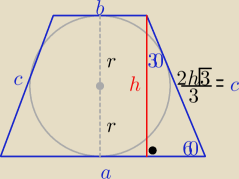Eta: h_p=2r=20

	h√3
z warunku wpisania okręgu w trapez : a+b= 2c , c=
	3

	a+b
Pp=		*h ⇒Pp= c*2r
	2