proszę o sprawdzenie Anna: Spośród wszystkich prostokątów symetrycznych względem osi OY których dwa wierzchołki należą do wykresu funkcji f(x) = − x² + 4 a dwa do osi x wyznacz wierzchołki prostokąta o największym polu. Oblicz to pole. nie chodzi mi o rozwiązanie bo razwiązałam ale chodzi mi o wyznaczenie dziedziny czy to jest: dziedzina : x ∊ (0 , +∞) czy x ∊ ( −2 ; 2 )

Pytający: Czyli chodzi o prostokąty ABCD: A = (−a, 0) B = (a, 0) C = (a, f(a)) D = (−a, f(a)) a∊(0, 2)∪(2, +∞) Ujemne a odpadają, bo prostokąty są symetryczne względem OY, natomiast dla a=2 odpowiednio wierzchołki A i D oraz B i C się pokrywają, więc nie powstanie z nich prostokąt. Wtedy: Pole_ABCD = |AB|*|AD| = 2a*|f(a)| lim_a→∞(2a*|f(a)|) = ∞ Stąd jasno wynika, że prostokąt o największym polu nie istnieje...

Anna: niestety wynik pola jest

	32√3
P =		i taki wynik otrzymałam
	9

A=(−x:0) B=(x; 0) C = ( −x ; −x² + 4 ) D( −x ; −x² + 4) P_Δ = IABI*IBCI P_Δ = 2x(−x² + 4) = − 2 x³ +8x P^,(x)= − 6x² + 8

	4		2√3		2√3
− 6x2 + 8 = 0 ⇔ x2 =		⇔ x1 =		x2 = −		ten nie należy do
	3		3		3

dziedziny

	32√3
i dla x1 pole =
	9

tak to zrobiłam

===: zapisana przez Ciebie treść zadania precyzyjna nie jest i jestem niemal pewny, że zapisałaś ją "swoimi słowami"

Pytający: Anno, prawdopodobnie jest to po prostu źle ułożone zadanie (bądź pomieszałaś treść), gdyż w Twych obliczeniach jest błąd. |AB| = √(x−(−x)²)+(0+0)²=|2x| |BC| = √(x−x)²+(−x²+4−0)²=|−x²+4| Nie można ot tak pominąć wartości bezwzględnej przy liczeniu długości odcinka.

Anna: zadanie zostało dobrze napisane analizując myślę że trzeba tylko zapisać odpowiednie założenia

===: i już mnie nie dziwi reforma oświaty

Pytający:

	270		32√3
Wystarczy wziąć x=3, wtedy pole = 2*3*5 = 30 =		>
	9		9

Stwierdzam tylko, że jaki byś x nie wybrała, zawsze można znaleźć taki, dla którego pole prostokąta będzie większe. Nie Twoja wina, że ktoś ułożył bezmyślnie zadanie (zapominając, że długość odcinka nie może być ujemna). Peace

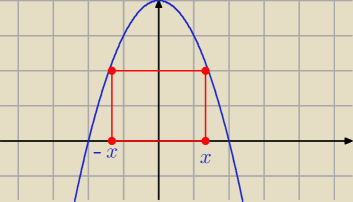
Janek191: x ∊ ( − 2, 2 ) P = 2* x*f(x) = 2x*( − x² + 4) = − 2 x³ + 8 x P(x) = −2 x³ + 8 x

	8		4
P'(x) = − 6 x2 + 8 = 0 ⇔ 6 x2 = 8 ⇔ x2 =		=
	6		3

	2		2 √3
x =		=
	√3		3

P ''(x) = − 12 x

	2√3
P ''(		) < 0
	3

	2 √3
Funkcja P(x) osiąga maksimum dla x =
	3

	2√3		32√3
Pmax = P(		) =
	3		9

====================================

Janek191: @ Pytający − nie mąć dziewczynie w głowie Wszystko jest ok

Anna: dziękuję

Kacper: Wszystko jest ok, o ile założymy że prostokąt na tylko dwa punkty wspólne z parabolą, a nikt o tym w treści nie wspomniał