Pole czworoboku
Bartek: Oblicz pole czworoboku o wierzcholkach O=(0,0,0) p=(0,0,2) q=(0,1,2) r=(0,2,1)
2 lut 12:36
Jerzy:
1) Sprawdź, czy nie jest to aby równoległobok ( jeśli tak, to banał)
2) Jeśli nie, to policz jako sume pól dwóch trójkątów ( wiecej liczenia)
2 lut 12:43
Bartek: Jak sprawdzic to to nie ronowleglobok?
2 lut 12:44
Jerzy:
Policz wektory i sprawdź, czy są parami równoległe.
2 lut 12:46
Bartek: Tzn:
PQ=(−1−3−4)
PR=(0,−1,1)
PS=(2,−1,−1)
I wyznacznik jest rowny 0, tzn., wiec jest rownoleglobokiem?
2 lut 12:49
Bartek: Na gorze zle nazwalem punkty jak cos
2 lut 12:51
Jerzy:
Jak Ty liczysz współrzędne wektora ?
2 lut 12:51
Bartek: X2−x1, y2−y2, moment bo nie do tego przykladu obliczylem
2 lut 12:55
Bartek: OP=(0,0,2) OQ=(0,1,2) OR=(0,2,−1)
2 lut 12:57
Jerzy:
Wszystkich wektorów jest 6.
2 lut 13:03
Kk: o to chodzi?
OP=(0,0,2) OQ=(0,1,2) OR=(0,2,1)
PR=(0,2,−1) QR=(0,1,−1) PQ=(0,1,0)
2 lut 13:16
Jerzy:
Tak . Czy są parami równoległe ?
2 lut 13:20
bartek: Jak to sprawdzic?
2 lut 13:24
bartek: X sa takie same , wiec chyba tak.
2 lut 13:27
Jerzy:
Najprościej ... sprawdzasz, czy któryś z wektorów jest iloczynem innego przez liczbę.
2 lut 13:27
Bartek: Dasz jakiś przyklad?
2 lut 13:38
Jerzy:
Np: [0,0,2] jest równoległy do [0,0,4] , bo: [0,0,4] = 2*[0,0,2]
2 lut 13:45
jc:
Punkty 0, u, v, u+v tworzą równoległobok, a tak przecież jest w zadaniu.
2 lut 14:22
jc: Głupoty piszę.
O=(0,0,0) p=(0,0,2) q=(0,1,2) r=(0,2,1)
Nie jest to równoległobok. Wszystkie wierzchołki leżą w jednej płaszczyźnie x=0.
Proponuję odczytać pole z rysunku.
2 lut 14:29
Jerzy:
Też byłem zdziwiony , jak Ci wyszedł równoległobok
2 lut 14:30
Jerzy:
Myślę,że on to musi zrobic rachunkami w przestrzeni.
2 lut 14:31
Mila:
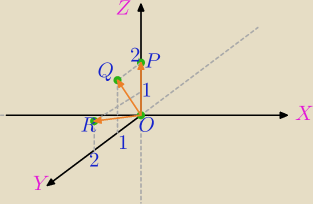
O=(0,0,0) ,P=(0,0,2), Q=(0,1,2), R=(0,2,1)
ΔOPQ− trójkąt prostokątny
albo tak:
OP
→=[0,0,2]
OQ
→=[0,1,2]
OR
→=[0,2,1]
| | 1 | | 1 | |
PΔOPQ= |
| *| [0,0,2] x [0,1,2] |= |
| *|−2i|=1 |
| | 2 | | 2 | |
| | 1 | | 1 | | 3 | |
PΔOQR= |
| *| [0,1,2] x [0,2,1 |= |
| *|−3i|= |
| |
| | 2 | | 2 | | 2 | |
P
OPQR=1+1.5=2.5
2 lut 18:30