rownanie parametryczne plaszczyzny Kuba: Wyznaczyc rownanie parametryczne plaszyczny π, ktora przechodzi przez punkt P = (1, −1, 1) oraz jest rownloległa do plaszczyzny π₂ : x + 2y + 2z = 0 Z góry dziekuje za pomoc

Adamm: n=[1; 2; 2] (x−1)+2(y+1)+2(z−1)=0 nie wiem jakie to jest parametryczne, to zrób sam

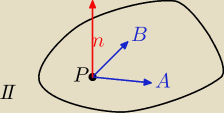
Mila: π: x+2y+2z−1=0 P=(1,−1,1) Szukamy dwóch punktów , które nie sa współliniowe z P z=0 x+2y−1=0 dla x=−3 mamy: −3+2y−1=0 A=(−3, 2,0) y=0 wtedy x+2z−1=0 dla x=3 mamy 3+2z−1=0 B=(3,0,−1) PA^→=[−4,3,−1] PB^→=[2,1,−2] π: x=1−4t+2s y=−1+3t+s z=1−1t−2s t,s∊R spr. [−4,3,−1] x [2,1,−2]=[−5,−10,−10] || [1,2,2]

Kuba: tylko skąd D = −1 w rownaniu plaszczyzny?

Mila: (x−1)+2(y+1)+2(z−1)=0⇔ x−1+2y+2+2z−2=0 x+2y+2z−1=0