pole trójkąta jc: Dla jakich dodatnich całkowitych n pole trójkąta o wierzchołkach (n+1,0,0), (0,n,0), (0,0,1) jest liczbą wymierną? całkowitą?

Benny: Dla żadnych n pole nie jest liczbą całkowitą. Chyba, że coś źle policzyłem.

	n2+3n+1
P=
	2

jc: Ale za to zawsze mamy liczbę wymierną. Wyszło mi podobnie. P=(n²+n+1)/2.

Benny: Ja to liczyłem wyznacznikiem.

jc: Pokaż swój rachunek

Jack: v = [n+1,−n,0] u = [0,−n,1] u x v = [−n,−n−1,−n(n+1)] |u x v| = √n² + (n+1)² + n²(n+1)² = = √n² + n² + 2n + 1 + n⁴ + 2n³ + n² = = √n⁴ + 2n³ + 3n² + 2n + 1 = √(n²+n+1)² = = n² + n + 1

	n2 + n + 1
P =
	2

?

jc: b.d.b.

jc: A teraz obliczmy pole czworościanu o wierzchołkach (0,0,0), (n+1,0,0), (0,n,0), (0,0,1) a jeszcze lepiej (0,0,0), (n,0,0), (0,n−1,0), (0,0,1). Wynik wygląda interesująco, choć może coś pomyliłem.

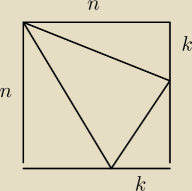
jc: W ten sposób z kwadratu nxn możemy utworzyć czworościan o wierzchołkach (0,0,0), (n,0,0), (0,n−k,0), (0,0,k). Daszek oczywiście będzie miał pole = n²−nk/2 −n(n−k)/2 − k(n−k)/2 = (n²−nk+k²)/2. I tajemnica się wyjaśniła ...