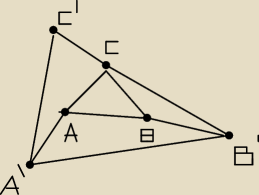
Planimetria-trojkaty, dowod Fanabela: Dane są trójkąty ABC i A'B'C' takie, że ptk C i A' są symetryczne względem A, ptk A i B' względem B, a ptk B i C' względem C. Pole trójkąta ABC jest rowne S. Wykaż, że pole trójkąta A'B'C' jest rowne 7S. Próbowałam z wzorem na pole trójkąta z sinusem (oznaczylam kąty wewnątrz ABC jako α,β i (180−α−β), ale to chyba zła droga. Myślałam jeszcze o wzorze Herona, ale to chyba też nic nie da. Bardzo proszę o wytłumaczenie

===: ... tylko porządny rysunek Cię uratuje

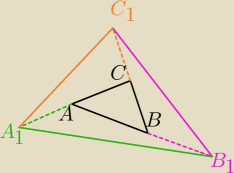===: zauważ, ze pole Δ_A1CC1 jest dwa razy większe od pola Δ_ABC pole Δ_AA1B1 jest dwa razy większe od pola Δ_ABC pole Δ_BB1C1 jest dwa razy większe od pola Δ_ABC a 2+2+2+1 to nie inaczej niżeli 7

===: dodatkowa podpowiedź

1		1
	a*bsinα=2*		2a*bsin(180o−α)
2		2

Fanabela: Przyznaje − rysunek faktycznie mi nie wyszedł ale nie rozumiem z czego wynika, to że te pola są dwa razy wieksze

Fanabela: Ok, juz rozumiem, bardzo dziekuje − sama pewnie bym na to nie wpadła i dalej walczylabym z heronem Jeszcze raz dziękuję

===: wiedziałem patrz "dodatkowa podpowiedź"

===: