Algebra :) Metis: Kilka zadań z algebry Przepraszam, że ich nie przepisuję, ale możecie mnie pokierować jak rozwiązać takie zadania?: http://image.prntscr.com/image/2a41b2d3369b46d3b6c491efe4867ad0.png http://image.prntscr.com/image/beb308a22d97429d9fb226097b2a1da0.png http://image.prntscr.com/image/65a5e93a65a44e879e7e375cd2838c73.png

Adamm: http://image.prntscr.com/image/2a41b2d3369b46d3b6c491efe4867ad0.png utwórz prostą z położenia kotka i kierunku w którym się porusza sprawdź punkt przecięcia

Metis: Opuściłem ten jeden wykład i nie wiem o czym mówisz Możesz pokazać mi na tym przykładzie co się robi, z pełnym opisem bym mógł sobie to przyswoić?

Jack: Ostatni link zadanie 1: Nalezy utworzyc plaszczyzne przechodzaca przez 3 punkty M, P, J nastepnie policzyc odleglosc punktu od plaszczyzny ze wzoru (teraz nie pamietam jak to szlo) w kazdym razie ta plaszczyzna : wyznaczamy wektor MP, nastepnie PJ i z iloczynu wektorowego tych wektorow mamy wektor normalny plaszczyzny czyli [A,B,C] nastepnie podstawiajac wspolrzedne dowolnego punktu obliczymy D. Rownanie plaszczyzny to A*x + B*y + C*z + D = 0 gdzie x,y,z to wspolrzedne punktu nalezacego do plaszczyzny Ostatni link zad. 2 mamy prosta ktorej wektor kierunkowy to [2,−1,1] oraz punkt do niej nalezacy K. Czyli mamy juz rownanie prostej Wyznaczamy z punktow MWP plaszczyzne, i liczymy punkt przebicia plaszczyzny z prosta. Plaszczyzne wyznaczamy jak wczesniej wektor MW, wektor WP, iloczyn wektorowy tych dwoch da nam wektor normalny plaszczyzny nastepnie podstawiajac dowolny punkt M,W lub P otrzymujemy rownanie ogolne plaszczyzny

Adamm: tworzysz prostą r(t)=t*[3; −1; 1]+[5; −8; 1]=[3t+5; −t−8; t+1] podstawiasz do obu płaszczyzn, masz punkt przecięcia (o ile się przecinają) liczysz odległość od K do punktu przecięcia

Metis: Dzięki Potem będę wstawił jeszcze inne zadanka do sprawdzenia, więc jeśli będziesz to rzucaj na nie okiem

Jack: srodkowy link : punkty M i W musza nalezec do plaszczyzny. oraz wiemy, ze przez ta plaszczyzne przechodzi prosta ktorej wektor kierunkowy to [3,−1,2] naszym zadaniem jest wyznaczyc plaszczyzne i potem obliczyc odleglosc punktu K od tej plaszczyzny (jest na to wzor−odleglosc punktu od plaszczyzny, poszukaj w internecie ) A te plaszczyzne mozemy np. tak : wyznaczamy wektor MW, mamy juz dany wektor [3,−1,2] zatem z iloczynu wektorowego tych dwoch wektorow otrzymamy wektor normalny plaszczyzny i potem podstawiajac punkt mamy plaszczyzne.

Jack: jakbym cos skopal to mowcie smialo

Mila: 9) l: 2x+y−z+7=0 x−y+3z−2=0 1) Równanie parametryczne prostej: z=t, t∊R 2x+y=−7+t x−y=2−3t −−−−−−−− l:

	5		2
x=−		−		t
	3		3

	11		7
y=−		+		t
	3		3

z=t

	2		7
l→=[−		,		,1] || [2,−7,−3]
	3		3

======================== 2) k^→=[3,−1,1] wektory k i l nie są równoległe prosta k: K=(5,−8,1)∊k x=5+3s y=−8−s z=1+s, s∊R 3) sprawdzamy czy proste przecinają się

	5		2
5+3s=−		−		t
	3		3

	11		7
−8−s=−		+		t
	3		3

1+s=t podstawiamy do 1 i 2 równania −−−−−−−−−−−−−−−−−−− 5+3s=−5/3−2/3*(1+s) −8−s=−11/3+7/3*(1+s)⇔ s=−2 i t=−1 P=(5+3*(−2),−8+2,1−2)=(−1,−6,−1)− punkt przecięcia prostych

	5		2		11		7
Wg drugiego wzoru P=(−		−		*(−1),−		+		*(−1),−1)=(−1,−6,−1)
	3		3		3		3

K=(5,−8,1) |PK|=√6²+2²+2²=√44=2√11 sprawdzajcie rachunki.

Metis: Milu

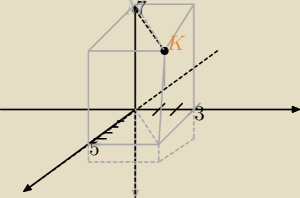
Mila: Mleko, kot, kłębek wełny: M=(1,0,−1) W=(2,4,−1) WM^→[−1,−4,0] w=[−3,−1,2] n^→[−1,−4,0] x [−3,−1,2]=[−8,2,−11] ||[8,−2,11] π: 8*(x−2)−2*(y−4)+11*(z+1)=0 8x−2y+11z+3=0

	|8*3−2*5+11*7+3|		94
d(K,π)=		=
	√82+22+112		3√21

tu też sprawdzajcie rachunki.