stereometria i zadanie optymalizacyjne

stereometria i zadanie optymalizacyjne Pati18773: Z kuli o promieniu długości R wytoczono walec o możliwie największej objętości. Wyznacz wymiary walca. Myślałam aby przyrównać do siebie objętość kuli i walca ale nie jestem pewna

1 lut 15:22

XL: walec o kwadratowym przekroju

1 lut 15:32

Pati18773: czemu tak ?

1 lut 15:34

Jack: Zakladamy ze wytoczono go bez zadnych strat, czyli objetosci sa rowne. ?

	4
V_k =		π R³
	3

V_w = π r² h V_k = V_w

4
	π R³ = π r² h
3

4
	R³ = r²h
3

4 
R3
3 

h =

r2

4 
R3
3 

Vk(r) = π r2 * 

r2

pochodna itd Tylko nwm czy o to chodzi w tym zadaniu, wytoczono walec...hmm

1 lut 15:49

Jerzy:

	4
@Jack ... u Ciebie: V_k(r) =		πR³ ... i pochodna: V'_k(r) = 0
	3

1 lut 15:53

Pati18773: raczej muszą być jakieś straty bo dalej w zadaniu muszę policzyć jaki procent objętości kuli stanowią odpady ale z tym dam sobie rade xd

1 lut 15:55

Jerzy: rysunek

I teraz licz...

1 lut 15:58

Pati18773: nie wiem co mi to daje

1 lut 16:01

Pati18773: a chwila chyba załapałam xd

1 lut 22:47

Pati18773:

	1
V(H)=π(R²−		H²)*H
	4

1 lut 22:53

Jerzy: Uzależnij objetosc walca od jednej zmiennej − kąta.

1 lut 22:54

Pati18773: R jest dane wiec nie mogę tak ?

1 lut 22:55

Jerzy: R to stała.

1 lut 23:19

Pati18773: no i nie uzależniłam od H ?

1 lut 23:21

Jerzy: Uzależnij objetosc od kata jaki tworzy promien kuli z podstawa walca

1 lut 23:22

Jerzy: A ilre Twoje H wynosi i jak się zmienia ?

1 lut 23:22

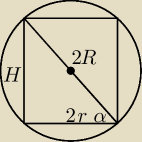
Pati18773: rysunek

mam takie rysunek

	2r
cosα=
	2R

r=cosαR

1 lut 23:29

Mila: Czy to jest dokładnie podana treść zadania?

2 lut 00:00

Mila: Może tak? W kulę o promieniu długości R wpisano walec o największej objętości....

2 lut 00:02

jc: Mila, nie wyobrażasz sobie, jak można wytoczyć z kuli walec?

	Objętość kuli
Wzór Pati z 22.53 daje V=		, czy coś podobnego.
	√3

2 lut 00:07

jc: a= h/2 r² + (h/2)²= R² V = πr²h R²/3=[r²/2 + r²/2+(h/2)²] / 3 ≥ [r⁴h²/16]^1/3 = V^2/3 /π^2/3/2^4/3 Równość mamy dla r²=h²/2. Wniosek V ≤ (π^2/3 2^4/3 R²/3)^3/2 = 4/3 πR /√3 = (obj. kuli)/√3 Skorzystałem z nierówności pomiędzy średnimi.

2 lut 00:26

Jerzy:

r
	= cosα ⇔ r = Rcosα
R

h
	= sinα ⇔ h = 2Rsinα
2R

V_w = πr²h = πR²cos²2Rsinα = 2R³cos²αsin²α

	π
Funkcja osiąga maksimum dla α =		, czyli najwiekszą objetość ma walec
	4

o przekroju kwdratu.

2 lut 08:12

XL: no i wyszło na moje a tyle sie naliczyliście

2 lut 11:34

Jerzy: To było wiadome z góry , ale uczeń nie może tak takiej odpowiedzi emotka

2 lut 11:36

Pati18773: skąd jest sin²α ?

2 lut 13:34

Jerzy: Pomyłka ..miało być: sinα

2 lut 13:35

Pati18773: Dobra. To teraz mam liczyć pochodną tego ?

2 lut 13:37

Jerzy: Tak.

2 lut 13:43

jc: Dla kwadratu mamy h=√2R, r=R/√2 V = πhr² = π R³ /√2. W przypadku h=√2r, r=√2/3R, h=2/√3 R, V=πhr² = π 4/(3√3) R³. 1/√2 < 4/(3√3) emotka

Mój walec jest większy! Jest największy.

2 lut 13:44

Pati18773: dobra to jeszcze jak obliczyć pochodna cos²α bo tego w szkole nie miałam

2 lut 13:48

Pati18773: (cos²α)'=−2sin(α)cos(α)

2 lut 13:54

Pati18773: czy tak ?

2 lut 13:54

Jerzy: Tak.

2 lut 13:56

Pati18773: pochodna wyszła mi V'=−4πR³cos²(α)sin(α)

2 lut 13:57

Jerzy: Niestety nie tak.

2 lut 14:00

Pati18773: R³ zostaje bez zmian ?

2 lut 14:03

Jerzy: To pochodna iloczynu: V'(α) = 4πR³*(cos²α*sinα)'

2 lut 14:05

Pati18773: a ja to wzięłam oddzielnie

dobra spróbuje coś wykombinować

2 lut 14:06

Pati18773: (cos²α*sinα)'=(cos²α)'*sinα+cos²α*(sinα)'=−2sinα*cosα*sinα+cos²α*cosα=−2sin²α*cosα+cos³α

2 lut 14:11

Jerzy: Teraz dobrze.

2 lut 14:13

Jerzy: Oczywiście stała przed nawiasem.

2 lut 14:14

Pati18773: a jak wyznaczyć dziedzinę ?

2 lut 14:16

Pati18773: tak tak stała przed xd

2 lut 14:17

Jerzy: Wszystko na nic ... też się zasugerowłem,że to będzie kwadrat.

	2√3
Walec ma najwiekszą objętość, gdy: H =
	3

Tutaj masz rozwiazanie prostsze niż z kątem α: https://www.zadania.info/289240

2 lut 14:27

Pati18773: czyli tak jak ja robiłam wcześniej wczoraj o 22.53

2 lut 14:29

jc: Rozwiązanie podałem przecież o 0:26. Wcześniej wspomniałem, że wynik wynika również ze wzoru Pati z 22.53.

2 lut 14:32

Jerzy: Dokładnie tak emotka

2 lut 14:32

Pati18773: dobra to teraz się zrobi

2 lut 14:34

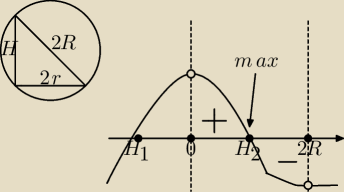
Pati18773: rysunek

Z kuli o promieniu długości R wytoczono walec o możliwie największej objętości. Wyznacz wymiary walca. Jaki procent objętości kuli stanowią odpady ?

	1
H²+(2r)²=(2R)² ⇒ r²=R²−		H²
	4

Szukamy r,H aby V była największa V=πr²H

	1
V(H)=π(R²−		H²)*H
	4

	1
V(H)=π(R²H−		H³)
	4

	1
r²>0 ⇒ R²−		H² ⇒ H<2R ⋁ H>−2R
	4

H>0 dziedzina: H∊(0;2R)

	3
V'(H)=π(R²−		H²)
	4

	3
wk: π(R²−		H²)=0
	4

	3
R²−		H²=0
	4

	4
H²=		R²
	3

	2√3		2√3
H₁=−		R ⋁ H₂=		R
	3		3

	2√3
V'(H)>0 dla H∊(0;		R) − funkcja rosnąca
	3

	2√3
V'(H)<0 dla H∊(		R;2R) − funkcja malejąca
	3

	2√3
to dla H=		R funkcja przyjmuje wartość największą
	3

	H²		2
r²=R²−		=		R²
	4		3

	2√3
r=		R
	3

	47√3R³
V(H)=π
	72

procent jaki stanowią odpadki wyszedł mi po ciężkich obliczeniach 15.2%

2 lut 15:39

Pati18773: nie tak V(H) już poprawiam

2 lut 15:48

Pati18773:

	4√3
V(H)=		πR³
	9

2 lut 15:50

Jerzy: I terz policz jaki procent stanowi odpad.

2 lut 15:52

Pati18773: i teraz odpadki stanowią 42,2% czy to możliwe

2 lut 15:54

Jerzy:

	√3
Nie: (4/9√3πR³):(4/3πR³) =		*100%
	3

2 lut 15:56

Pati18773: a ja odejmowałam objetosc kuli − objetość walca

2 lut 16:03

Mila: To w końcu rozwiązałaś to zadanie, bo tyle tu komentarzy..

2 lut 19:18

Pati18773: rozwiązane XD

3 lut 01:07

Jerzy: Od objętośći kuli odejmij objętość walca, to będzie odpad. Potem policz jaki procent objetości kuli stanowi odpad.

3 lut 09:20