Funkcja wykładnicza Michał: Dla jakich wartości parametru m dane równanie ma pierwiastek dodatni: a) 9^x = m + 1 b) (^√2₂)^x = 2^m c) 2x + 4 = 2^{m − 1} W pierwszym wypadku jest x > 0, czyli m + 1 > 1, czyli m > 0; W drugim m = − ¹₂, więc m < 0, aby wynik był dodatni; Jak rozwiązać podpunkt c) i czy dobrze myślę w dwóch poprzednich?

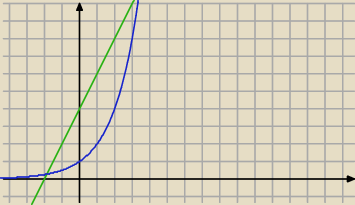
Jerzy: a) i b) − dobrze c) − popatrz na wykresy

Michał: Czy chodzi o to, że punkt przecięcia z osią OY funkcji liniowej wynosi (0;4)? I wtedy szukam parametru m, dla którego funkcja wykładnicza będzie miała wartość większą od 4. Czyli 2^m−1 > 4, i z tego wychodzi m > 3. Zgadza się?

Jerzy: Popatrz uważnie .. .czy jest możliwym, aby wykres funkcji liniowej przeciął wykres prostej dla x < 0 ?

Jerzy: ...wykres funkcji wykładniczej przeciął wykres prostej...

Michał: No nie. Ale czy moje rozumowanie powyżej jest właściwe? Znaczy że biorę miejsce w którym funkcja liniowa przecina OY i porównuję tą wartość do funkcji wykładniczej. Nie wiem jak poradzić sobie z logarytmami w mianowniku: Uzasadnij równość: 2 / (log_2√23 + 1 / (log₄9) = 4 log₃2 Doprowadzam do wspólnego mianownika, ale nie wiem co zrobić z mnożeniem logarytmów.

Jerzy: Funkcja wykładnicza zawsze bedzie przecinać tą prostą dla x > 0. Z lewej strony zmień podstawy logarytmów

Adamm: zadanie: dla jakich m istnieje x>0 spełniające równanie 1) funkcja jest rosnąca, x>0 implikuje 9^x>1 czyli m+1>1 stąd m>0

	√2
2) funkcja malejąca, x>0 implikuje (		)x<1 czyli 2m<1 stąd m<0
	2

3) x>0 implikuje 2x+4>4, stąd 2^m−1>4 czyli m−1>2, m>3