Zadania z wektorami Deiv: Witam, pomoglby ktos rozwiazac ponizsze zadania? :c 1. Obliczyc obj. rownolegloscianu o wierzcholkach O=(0,1,1) P=(0,1,3) Q=(0,2,3) R=(1,3,2) 2. Znalezc wektor jednostkowy m prostopadly do wektorow a = (1,0,−2) b=(1,1,0) 3.Wykazac, ze punkty O=(2,1,0), P=(4,1,0), Q=(4,2,0), R=(3,2,0) sa wierzcholkami trapezu. Obliczyc jego pole.

Jerzy: 1) V = I(OP x OQ) o OR|

Jerzy: 3) 1) Pokazać ,że punkty leżą w jednej płaszczyżnie 2) Pokazać,że dwie proste są równoległe 3) Obliczyć odległość między nimi 4) Obliczyć długość podstawy 5) Obliczyc pole trapezu.

Jerzy: 2) Znajdź wektor prostopadły do danych i podziel go przez jego długość.

Deiv: Czyli w tym drugim: | i j k | | 1 0 −2 | = ( |0 − 2| | 1 −2 | |1 0 |) = (2,2,1) | 1 1 0 | ( |1 0 |, | 1 0 |, | 1 1|) i podzielic przez dlugosc tego nowego wektora ? √2²+2²+1²=√9=3 ?

Jerzy:

1
	[2,−2,1]
3

Deiv: w 3) OP=(2,0,0) − dolna podstawa QR=(−1,0,0) − gorna podstawa OR=(1,1,0) QR=(0,1,0) W jaki sposob sprawdzic czy podstawy sa rownolegle?

Jerzy: Sprawdź, które wektory kierunkowe są równoległe ( to będą podstawy trapezu)

Deiv: Rownolegle sa OP i QR − to sa wlasnie te podstawy

Jerzy: Nie zauważyłem ...OP II QR

Jerzy: Tak, to są podstawy.

Jerzy: Wysokość trapezu obliczysz dzieląc pole równoległoboku zbudowanego na wektorach OP i OR prze długość wektora OP ( to odległość miedzy prostymi OP mi QR

Deiv: moglbys napisac w przykladzie jak wyliczyc ta wysokosc, bo nie moge ogarnac

Deiv: P trapezu to P=((a+b)/2)*h dlugosc podstawy QR to 1 dlugosc podstawy OP to 2 a wysokosc?

Jerzy: P = IOP x ORI − pole równoległoboku = długość tego wektora i potem dzielisz to pole przez długość wektora OP ( to bedzie odległość tych prostych,czyli wysokość trapezu )

Deiv: Czyli: P=|OP x OR| = (0,0,2) i to podzielic przez dlugosc wektora OP czyli przez 2 ?

Deiv: OP=(2,0,0) |OP|=√2²+0²+0²=2

Deiv: A nie lepiej obliczyc pole tego trapezu, dzielac go na trojkaty i : 1/2|OP x OR\ + 1/2 |QR + OP| ?

Jerzy: Teraz widzę,że masz źle policzone wektory już na poczatku zdania, czyli wszystko dalej jest do bani.

Jerzy: A nie ... spojrzałem na punkty z pierwszego zadania.

Jerzy: Jednak masz bałagan.. OP = [2,0,0] OQ = [2,1,0] OR = [1,1,0] PQ = [0,1,0]

Deiv: Na pewno OQ ma byc ?

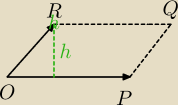
Jerzy: Pole równoległoboku = |OP^→ x OR^→|

Deiv: |OP X OR| = (0,0,2) i to koniec?

Deiv: |OP X OR| = (0,0,2) i to koniec?

Deiv: |OP X OR| = √4=2...