Dowód
Patryk: Udowodnić, że dla każdego n∊N zachodzą nierówności
| | 1 | | 1 | | 1 | |
2(√n+1−1)< |
| + |
| +...+ |
| <2√n |
| | √1 | | √2 | | √n | |
Proszę o jakąś podpowiedź, bo nie wiem jak to ugryźć

31 sty 12:00
g:
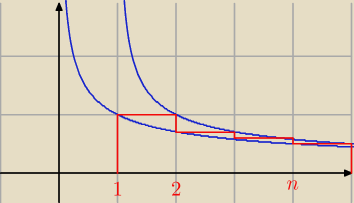
| | 1 | | 1 | |
∫1n+1 |
| dx < S < ∫1n+1 |
| dx |
| | √x | | √x−1 | |
31 sty 12:58
Patryk: Całek jeszcze nie miałem.
31 sty 13:06
Adamm: spróbuj indukcyjnie
31 sty 14:10
Patryk: indukcyjnie oddzielnie te nierówności?
31 sty 14:12
Adamm: tak
31 sty 14:13
Patryk: Dzięki wyszło.
31 sty 17:07

