ohh
cynamonek: długość wysokosci rombu jest równa 6 a cosinus kąta ostrego wynosi 25 oblicz przekątne.
30 sty 18:54
Adamm:
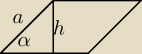
jedną z przekątnych możesz łatwo obliczyć twierdzeniem cosinusów
drugą na przykład twierdzeniem Pitagorasa
30 sty 18:58
Janek191:
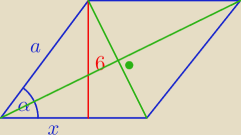
30 sty 18:59
cynamonek: czemu h przez a równa się 2 przez 3?
30 sty 19:16
Janek191:
Adamm: się pomylił

Ma być
30 sty 19:19
30 sty 19:21
cynamonek: Do tego miejsca też doszedłem i za bardzo dalej nie wiem co zrobić. Z tego działu kompletnie
nic nie ogarniam. Chyba, że trójkąty

Czy ta jednak przekątna tworzy tutaj trójkąt równoramienny?
30 sty 19:33
Adamm: mówiłem jak możesz to łatwo zrobić
z twierdzenia cosinusów
p2=a2+a2−2a2cosα
dalej możesz policzyć drugą przekątną stosując tw. Pitagorasa
30 sty 19:35
Adamm: albo możesz przyrównać pola
30 sty 19:39
30 sty 19:41
Janek191:
| x | | 2 | | 2 | | 4 | |
| = |
| ⇒ 3 x = 2 a ⇒ x = |
| a ⇒ x2 = |
| a2 |
| a | | 3 | | 3 | | 9 | |
Tw. Pitagorasa
x
2 + 6
2 = a
2
| | 4 | | 5 | |
36 = a2 − |
| a2 = |
| a2 / * 9 |
| | 9 | | 9 | |
5 a
2 = 36*9
p
1 − długość krótszej przekątnej
Mamy
| | 72*9 | | 72*9 | | 2 | |
(p1)2 = a2 + a2 − 2 a2 cos α = |
| − |
| * |
| = ... |
| | 5 | | 5 | | 3 | |
30 sty 19:43
Janek191:
| | 2 | | 2 | |
cos α = |
| , czy cos α = |
| ? |
| | 3 | | 5 | |
30 sty 19:46
5-latek: Witaj
Janek191 
| | 2 | |
jest |
| ale to nie ma znaczenia wielkiego . |
| | 5 | |
Ma schemat niech dziala
30 sty 19:48
Janek191:
Witaj !
Ja nie dowidzę

30 sty 19:56
Jolanta: To zasługa ,myzianego" ekranu. Powiekszam przy ułamkach

30 sty 20:09
cynamonek: heh dobra dzięki

30 sty 20:14


 Ma być
Ma być
 Czy ta jednak przekątna tworzy tutaj trójkąt równoramienny?
Czy ta jednak przekątna tworzy tutaj trójkąt równoramienny?



