algebra liniowa
czeko: Witam mam dwa takie przykłady proszę o rozjaśnienie:
| | 1 | | √3 | |
1) (z − 1)4 = |
| +i |
| |
| | 2 | | 2 | |
| | 3 | | 4 | |
2) (2z − 2)4 = ( |
| − i |
| )8 |
| | 5 | | 5 | |
30 sty 11:17
czeko: ktoś ma może jakiś pomysł?
30 sty 17:31
czeko: czy ktoś mógłby mi pomóc?
31 sty 21:44
g:
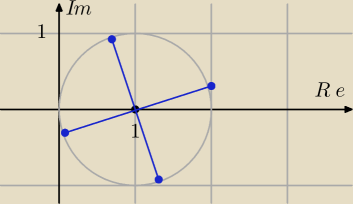
1)
| | 1/2 | |
|P| = √1/4+3/4 = 1, arg(P) = arccos( |
| ) = 60st = π/3 |
| | 1 | |
| | 2π | |
|z−1| = 4√|P| = 1, arg(z−1) = arg(P)/4 + |
| *k, k∊[0,3] |
| | 4 | |
z−1 = |z−1| * (cos(arg) + i*sin(arg))
2) podobnie
31 sty 22:36
czeko: a jak wyliczyć |z−1|

31 sty 22:43
czeko: nie do końca to rozumiem
31 sty 22:45
g: Już Ci policzyłem |z−1|.
31 sty 22:48
czeko: | | π | | π | |
czyli teraz pozostaje |z−1|*(cos(arg)+i*sin(arg)) = cos |
| + isin |
| |
| | 3 | | 3 | |
porównuję moduł i arg

31 sty 22:50
31 sty 22:52
czeko: raczej obliczam
1*(cos(arg) +isin(arg)) dla k ∊[0,3]
31 sty 22:55
 1)
1)

