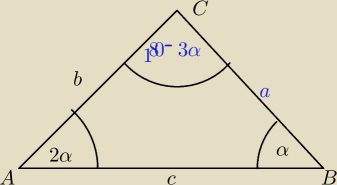
 W trojkacie ABC kat przy wierzchoklu A jest 2 razy wiekszy niz przy wierzcholku B
Boki AB o AC maja odpowiednio dlugosc c i b . Wyznacz dlugosc trzeciego boku
Chcialem to zrobic tak
3α+(180−3α)=180 i wyliczyc α ale ztego wychodzi mi ze α=0
W trojkacie ABC kat przy wierzchoklu A jest 2 razy wiekszy niz przy wierzcholku B
Boki AB o AC maja odpowiednio dlugosc c i b . Wyznacz dlugosc trzeciego boku
Chcialem to zrobic tak
3α+(180−3α)=180 i wyliczyc α ale ztego wychodzi mi ze α=0
| a | b | ||
= | |||
| sin2a | sina |
| b*sin2a | b*2sinacosa | |||
a= | = | =2bcosa | ||
| sina | sina |
| a | b | |||
1/ z tw. sinusów | = | ⇒ a=2bcosα | ||
| sin(2α) | sinα |
| b+c | b+c | |||
3/ i z tw. sinusów : bsinα(3−4sin2α)=csinα ⇒ 4cos2α= | ⇒ 2cosα=√ | |||
| b | b |
| b+c | ||
a=b*√ | = √b(b+c) | |
| b |

| a*sinα | ||
To tak z Twierdzenia sinusow oblicze bok b ⇒b= | = | |
| sin2α |
| a*sinα | 1 | |||
= | a cosα | |||
| 2sinαcosα | 2 |
| 1 | 1 | |||
a2= ( | a*cosα)2+c2−2* | acosα*cos2α | ||
| 2 | 2 |
| 1 | ||
a2= | a2cos2α+c2−acosα*cos2α | |
| 4 |
 i Aga1
i Aga1  Pisalem jak nie bylo Waszych postow .
Przeanalizuje sobie to co napisalyscie .
Pisalem jak nie bylo Waszych postow .
Przeanalizuje sobie to co napisalyscie .
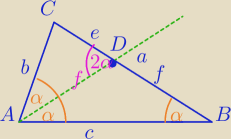 III)
AD− dwusieczna kąta A
1) ΔADC∼ΔABC
III)
AD− dwusieczna kąta A
1) ΔADC∼ΔABC
| b | a | ||
= | ⇔ | ||
| f | c |
| b*c | ||
a= | ||
| f |
| b | e | f*(b+c) | |||
= | , e+f=a ⇔a= | ||||
| c | f | c |
| b*c | f*(b+c) | ||
= | ⇔ | ||
| f | c |
| c*√b | ||
f= | ||
| √b+c |
| b*c | b*c*√b+c | |||
a= | = | ⇔ | ||
| f | c√b |
 Pozdrawiam
Musze sobie poczytac o tych twierdzeniach
Probuje robic te zadania ale czasami brakuje wiedzy i sprawnosci rachunkowej
Pozdrawiam
Musze sobie poczytac o tych twierdzeniach
Probuje robic te zadania ale czasami brakuje wiedzy i sprawnosci rachunkowej 
 .
Mam juz goracy termoform i zaraz bede sie wygrzewal .
.
Mam juz goracy termoform i zaraz bede sie wygrzewal .

 Mam nalewke truskawkową i chyba spozyje .
Mam nalewke truskawkową i chyba spozyje .