planimetria
hum: czy da podzielić kwadrat 8x8 kratek na 15 kwadratów (różnych rozmiarów)?
29 sty 15:14
SEKS INSTRUKTOR : da sie

29 sty 15:25
Janek191:
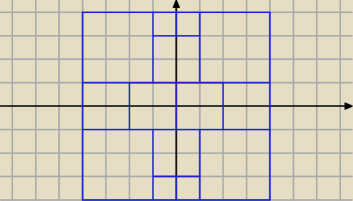
Podział na 14 kwadratów.
29 sty 15:41
Adamm: najpierw zastanówmy się czy 64 można przedstawić w postaci sumy 15 kwadratów
29 sty 15:46
hum: no właśnie, ale jak się za to zabrać

29 sty 17:22
an:
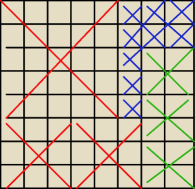
29 sty 18:19
hum: czyli się da

a da się to zrobić jakoś algebraicznie? wykazać, że 64 da się przedstawić jako sumę 15
naturalnych liczb kwadratowych?
29 sty 18:22
an: trochę ułatwia
x62+y52+z42+v32+u22+t=64
x + y + z + v + u + t =15
35x +24y +15z +8v +3u = 49
29 sty 18:39
hum: hm, nie rozumiem czemu tak

czemu akurat 6 niewiadomych?
29 sty 19:39
jc: Bo mogły się przecież pojawić kwadraty 6x6, a że się nie pojawiły ...
29 sty 20:05
hum: hm, i tak nie rozumiem

29 sty 21:03
an: 7 i same 1 za dużo
6 na wyrost wówczas 5,4,3 nie wchodza pozostaje 3u=14
5, to 4 się nie mieści pozostaje 8v+3u=25 spełnine tylko dla v=2
4 jedna to 8v +3u=34 spełnione dla v=2 u=6 t=6 da się rozmieścić
4 dwie to 8v+3u=18 v=0 u=6 powinno być t=7, ale w tm wypadku nie może być nieparzyste
4 trzy 8v+3u=1 odpada
3 , to 8v +3u=49 v=2 odpada,v=5 nie wchodzi w kwadrat 8*8
2 to 3u =49 nie dieli się
1 za dużo 1`
Czyli są dwa rozwiązania jeśli sie nie pomyliłem
29 sty 21:09

 Podział na 14 kwadratów.
Podział na 14 kwadratów.


 a da się to zrobić jakoś algebraicznie? wykazać, że 64 da się przedstawić jako sumę 15
naturalnych liczb kwadratowych?
a da się to zrobić jakoś algebraicznie? wykazać, że 64 da się przedstawić jako sumę 15
naturalnych liczb kwadratowych?
 czemu akurat 6 niewiadomych?
czemu akurat 6 niewiadomych?
