trójkąt Radek: W trójkącie prostokątnym równoramiennym ABC , |<BAC|=90^o i punkt M jest środkiem boku AB . Z punktu A poprowadzono prostą prostopadłą do BC,która przecina bok BC w punkcie N. Wykaż,że |<AMC|=|<BMN| Rysunek zrobiłem i nic pomożecie

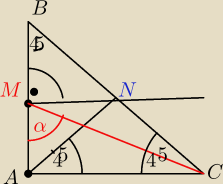
Krzysiek: Rysunek do zadania wedlug tresci Zrobiles i nie zauwazyles ze nie sa rowne ?

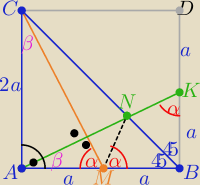
Eta: 1/ zbuduj kwadrat ABDC 2/ z treści zadania : AN⊥MC i M −− środkiem boku AB ⇒ K jest środkiem boku BD 3/ΔAMC≡ΔABK z cechy (bkb) ⇒ |∡AMC|=|∡AKB|=α 4/ΔBMN≡ΔBNK z cechy (bkb) −−−−−−− ( dodaj komentarz dlaczego? zatem |∡BMN|=|∡AKB|=α ⇒ ....... teza |∡AMC|=|∡BMN| c.n.w.

Eta: Duchem nie jestem ale (myślę,że w treści ma być: .... "prostopadłą do MC" Ciekawe jaki masz ten rysunek? ............

Krzysiek: Dobry wieczor Eta A co jest zle w moim rysunku do zadania ? Bo tak jesli trojkat prostokatny jest rownoramienny to prosta prostopadla do boku BC i wychodzaca a kata prostego dzieli podstawe BC na polowy N dzieli bok AB na polowe wiec w tym trojkacie prosta MN bedzie rownolegla do AC

Krzysiek: To w takim razie poczekajmy na Radka

Eta: @ Krzysiek według treści ,którą podał Radek : takie kąty nie mają równych miar! dlatego myślę ..... jak podałam wyżej

Krzysiek: I ja tez tak mysle ze bedzie tak jak Ty to zrobilas Bo to byloby za proste . Chcialbym Ci rowniez podziekowac za to rozwiazanie

Eta: