Oblicz kosinus kąta między punktami
xx: Dany jest czworobok o danych wierzchołkach:
A1(0,1)
A2(4,0)
A3(3,6)
A4(1,5)
Oblicz kosinus kąta A4 A1 A2
29 sty 12:05
Janek191:
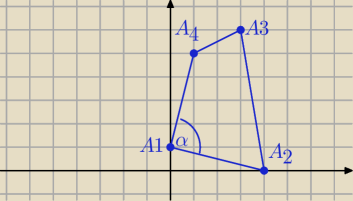
→ →
A
1A
2 = [ 4, − 1] = v
→ →
A
1A
4 = [ 1,4] = w
Iloczyn skalarny
→ →
v o w = 4*1 + (−1)*4 = 0
Wektory są prostopadłe, więc cos α = 0
29 sty 12:16
===:
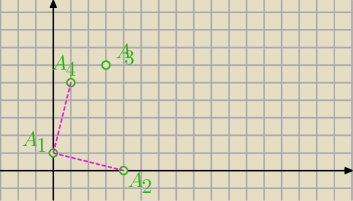
np tak:
Wnioski już dla Ciebie

29 sty 12:19
xx: A co by było w przypadku gdy nie są prostopadłe? W innej grupie należy policzyć cosinus między
A1 A2 i A3, z czego:
→ →
A2A1= [ −4, 1] = v
→ →
A2A3 = [ −1, 6]= w
Iloczyn skalarny
→ →
v o w = −4*(−1) + 1*6 = 10
29 sty 12:26
xx: podbijam pytanie
29 sty 12:41
29 sty 12:41
Janek191:
v , w − długości wektorów
29 sty 12:42
xx: Robiłam to tak ale wynik wyszedł mi...dziwny.
→ →
A2A1= [ −4, 1] = v
→ →
A2A3 = [ −1, 6]= w
→ →
v o w = −4*(−1) + 1*6 = 10
|v| = √−42 + 12= √17
|w| = √−12 + 62= √37
Po podstawieniu cosinus wychodzi mi
10
−−−−−−
√17√37
29 sty 12:56
Janek191:
Przy obliczaniu długości wektorów − 4 powinno być w nawiasie. Podobnie −1.
| | 10 | | 10 | |
cos β = |
| = |
| |
| | √17*√37 | | √629 | |
29 sty 12:59
 → →
A1A2 = [ 4, − 1] = v
→ →
A1A4 = [ 1,4] = w
Iloczyn skalarny
→ →
v o w = 4*1 + (−1)*4 = 0
Wektory są prostopadłe, więc cos α = 0
→ →
A1A2 = [ 4, − 1] = v
→ →
A1A4 = [ 1,4] = w
Iloczyn skalarny
→ →
v o w = 4*1 + (−1)*4 = 0
Wektory są prostopadłe, więc cos α = 0
 np tak:
np tak:
