Całka oznaczona - geometria lolek: Obliczyć pole powierzchni powstałej w wyniku obrotu wokół osi OX i linii równaniu y=√2x+x²

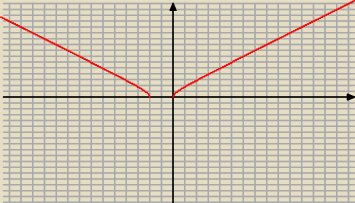
Adamm: pole powierzchni jest nieskończone od razu to widać, ale możesz się bawić jak chcesz

lolek: tymczasem w odpowiedziach jest 4pi ? (dla mnie to też jest nie skończone)

lolek: obliczyć pole powierzchni powstałej w wyniku obrotu dookoła osi OX linii równaniu ta sama linia

lolek: ?

jc: A może było tak y = √2x−x²?

Adamm: wtedy mogłoby tak być y²+x²−2x=0 y²+(x−1)²=1 górna część koła obracając wokół osi OX dostajemy kulę o promieniu 1, pole powierzchni to 4π

lolek: tak tak był minus , nie wiem skąd wychodzi wynik, jakieś wzory czy coś nie rozumiem tego zadnia

Adamm: wzór na pole powierzchni koła wystarczy P=4πr² r=1

Adamm: kuli nie koła

lolek: nawet jeśli mam zapisane że mam to całką obliczyć ? to stosuje wzór na pole koła ?

Adamm: nie, wtedy liczysz to całką 2π∫₀²√2x−x²√1+((√2x−x²)')²dx