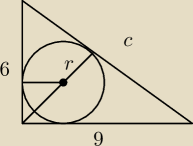
hmmm cynamonek: W trójkąt prostokątny o przyprostokątnych długości 6 i 9 wpisano okrąg. Oblicz długość odcinków na jakie dzieli przeciwprostokątną punkt styczności. Mój rysunek pomocniczy, Nie mogę sobie przypomnieć jak takie zadanie się robiło Czy ta średnica dzieli mi na trójkąt równo ramienny? Czy te 2 trójkąty są sobie równe? c= 3√13

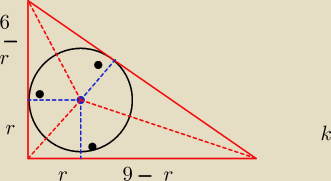
Gaunt: Środek okręgu wpisanego w Δ wyznaczają dwusieczne kątów Δ. Potrafisz coś na tej podstawie wywnioskować?

cynamonek: r√2 , górna jest 2 razy większa a trzecia jest 4 razy większa?

cynamonek: x ( przeciw prostokątna dolnego trójkąta) x² = 9² + ( r √2 + r)²

cynamonek: 9² = ( r √2 + r)2 + x² x − o jest przyprostokątna dolnego trójkąta

cynamonek: (9−r)² + r² = h² gdzie te h jest przeciwprostokątną i wyliczam z delty?

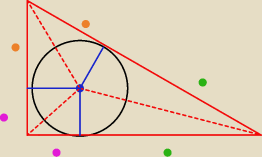
Gaunt: Można prościej: Ten trójkąt składa się z 3 par trójkątów przystających − mają takie same kąty (dwusieczne i kąty proste) i mają po 1 boku wspólnym − zasada BKB. Dlatego boki oznaczone tymi samymi kolorami są równej dlugości. 6−r+9−r=3√13 Obliczysz r − obliczysz długości boków − odpowiednio 6−r i 9−r