| 3 | ||
Posługując się wykresem funkcji f(x) = cos2x dla x∈(−π, − | π>, rozwiąż nierówność | |
| 2 |
| 5 | ||
opartego na | okręgu. | |
| 12 |
| 5 | ||
Jeśli miara kąta α jest równa mierze łukowej kąta środkowego okręgu opartego na | ||
| 12 |
| 5 | 5 | |||
okręgu, to α = | * 2π = | π | ||
| 12 | 6 |
| 5 | 1 | 1 | 1 | |||||
sin | π = sin(π − | π) = sin | π = | |||||
| 6 | 6 | 6 | 2 |
| 5 | 5 | |||
zadaniu α = | π, a więc należy rozwiązać nierówność: cos2x < sin | π, czyli | ||
| 6 | 6 |
| 1 | ||
cos2x < | . | |
| 2 |
| 1 | 3 | |||
Zadanie sprowadza się do rozwiązania nierówności: cos2x < | dla x∊(−π, − | π>. | ||
| 2 | 2 |
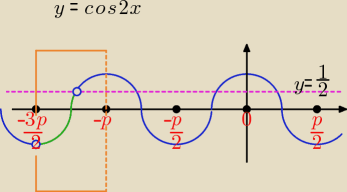 p oznacza π
Trzeba określić przedział argumentów funkcji y = cos2x dla zielonej części jego wykresu.
p oznacza π
Trzeba określić przedział argumentów funkcji y = cos2x dla zielonej części jego wykresu.
| 1 | ||
to według Ciebie (tam gdzie masz zaznaczony punkt przecięcia y= | ) ile wynosi ? | |
| 2 |
| 1 | 3 | |||
rozwiązujemy równanie: cos2x = | dla x∊<− | π, −π) | ||
| 2 | 2 |
| π | ||
cos2x = cos | ||
| 3 |
| π | π | |||
2x = | + k*2π lub 2x = − | + k*2π, k∊C | ||
| 3 | 3 |
| π | π | |||
x = | + k*π lub x = − | + k*π | ||
| 6 | 6 |
| 3 | ||
Dobieramy takie k∊C, aby x∊<− | π, −π) | |
| 2 |
| π | 5 | 3 | ||||
k = −1: x = | − π = − | π ∉ <− | π, −π) | |||
| 6 | 6 | 2 |
| π | 7 | 3 | ||||
x = − | −π = − | π ∊ <− | π, −π) | |||
| 6 | 6 | 2 |
| 3 | 7 | |||
odp.: x∊<− | π, − | π) | ||
| 2 | 6 |