Zadanie maturalne 8 p.r. Bogdan: Zadanie maturalne 8 (5 pkt)

	4
Wykaż, że cosinus kąta przecięcia się wykresów funkcji f(x) =		x + 1 i g(x) = −x√2 + 9
	3

	4√6 −3√3)
jest równy		.
	15

Myślę, że to zadanie dostarczy rozwiązującym wiele emocji

lena: NIE UMIEM TEGO NIE MAM POJęCIA OD CZEGO ZACZąć MAM 10 LAT PRZERWY

Julek: piszę

Julek: a₁ = 4/3 a₂ = −√2

	4   + √2 3
tgα =|		| =
	4√2 + 3   −   3

	4		3
= |(		+ √2) * (		)| =
	3		4√2 + 3

	4+3√2		(4+3√2)(4√2−3)
= |		| =
	4√2 + 3		23

teraz wyjdzie wynik,który będzie tg tego konta niestety, nie mogę dokończyć bo się śpiesze (chętnie, ale jutro). Oto wzory z których następnie trzeba skorzystać!

	sinα
tgα =		oraz sin2α+cos2α = 1
	cosα

Julek: kąta* // pośpiech

Bogdan: tgα został przez Julka wyznaczony błędnie, jest jednak prostszy rachunkowo sposób na

	a1 − a2
rozwiązanie tego zadania bez stosowania wzoru tgα = |		|
	1 + a1*a2

Julek: myślę, że gdybym wziął kartkę i spróbował tę zadanie rozwiązać jednak wykorzystując wzór doszedłbym do prawidłowego wyniku. A jestem ciekaw Bogdanie, o jakim sposobie piszesz Nie przychodzi mi na myśl...

Bogdan: Najpierw poprawimy tgα.

	4 + 3√2
tgα =
	4√2 − 3

Za bezbłędne doprowadzenie rozwiązania do tego miejsca z zastosowaniem wzoru na tg kąta zawartego między prostymi komisja egzaminacyjna przyzna 3 punkty. Na razie nie podaję rozwiązań zadań, niech inni też mają przyjemność w rozwiązywaniu.

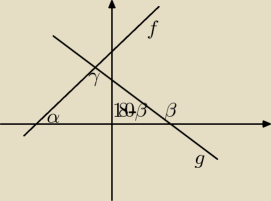mrówka_z: γ=180−(α+β−180)=180−α−180+β=β−α cos(β−α)=cosβcosα+sinβsinα tgα=4/3 4/3=sinα/cosα cosα=3/4sinα z jedynki trygonometrycznej: 1−cos²α=16/9cos²α cos²α=9/25 => cosα=3/5 sinα=4/5 ponieważ tgα>0 Takim samym sposobem liczę wartości funkcji sin i cos dla kąta β. sinβ=−√2cosβ 1−cos²β=2cos²β cosβ=−√3/3 sinβ=√6/3 ponieważ tgβ<0 Korzystam ze wzoru wyprowadzonego wcześniej: cosγ=cos(β−α)=−√3*3/5+√6/3*4/5=(4√6−3√3)/15 Po drodze oczywiście założenie, teza itp CNW

Eta: Ja podam takie rozwiązanie → f: ⁴₃*x −y+1=0 wektor u prostopadły do prostej f: u= [⁴₃, −1] → g: −√2 *x −y+9=0 " v " " " g: v=[−√2,−1] → → z iloczynu skalarnego : u o v= IuI*IvI*cos <(u,v) I<(u,v)I=φ IuI = ⁵₃ IvI= √3 to

	43*(−√2+(−1)*(−1)		−4√2+3
cosφ=		=
	53*√3		3*53*√3

	(−4√2+3)*√3		−4√6+3√3
cosφ=		=		<0
	15		15

cosφ<0 => φ€ ( 90^o, 180^o) bo φ kąt między prostymi zatem: cos ( 180^o −φ) = −cosφ

	4√6−3√3
to: −cosφ= −
	15

	4√6−3√3
to cosφ=
	15

c.b.d.o.