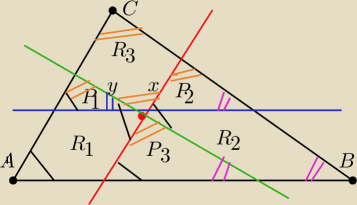
rownoleglobok i trojkaty 5-latek: Przez punkt lezacy wewnatrz trojkata poprowadzono 3 prosterownolegle do bolow trojakta proste te dziela trojkat na 3 trojkaty P₁ P₂,P₃ i trzy rownolegloboki R₁,R₂ R₃ WIedzac z epola otrzymanych rownleglobokow sa rowne odpowiednio P_r1 , P_r2 P_r3 znalezc pola powierzchni otrzymanych trojkatow Oznaczylem katy trojkata A, B C Oznaczylem boki rownolegloboku R₃ przez x i y Oznaczylem tez katy jako katy odpowiadajace (dwie proste rownolegle przeciete sieczna Pole rownolrgloboku = iloczyn dwoch bokow * sinus kata zawartego miedzy nimi We wskazowce jest Rozwazyc rownilegloboki i przylegle do nich trojkaty mamy wtedy 4P_p1*P_p2= P²_r3 4P_p2*P_p3= P²r1 4P_p1*P_p3= P²r2 Z tych rownan wyznaznaczamy

	pr2*Pr3
Pp1=
	2Pr1

	Pr1*Pr3
Pp2=
	2Pr2

	Pr1*Pr2
Pp3=
	2Pr3

Dlaczego tak jest( tam gdziejest to 4* .......) i czy dobrze oznaczylem katy ? 4P_p2*P_p3= P²r1

5-latek: Co zauwazylem to trojakty P₁ i P₂ sa rownoramienne P₁ o boku y i P₂ o boku x Natomiast dalej sie zastaniawiam nad trojkatem P₃

5-latek: Nie tak (napisalem bzdure

5-latek:

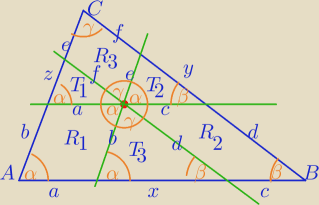Mila: wg oznaczeń na rysunku: Dla ułatwienia w zapisach: T₁− pole Δ1 R₁ − pole równoległoboku 1 R₁=a*b*sinα

	1		2T1
T1=		*z*a*sinα⇔sinα=
	2		z*a

	1		2T3
T3=		*b*x*sinα⇔sinα=
	2		x*b

	2T1		2T3
R12=a2*b2*sin2α=a2*b2*sinα*sinα=a2*b2*		*		⇔
	z*a		x*b

	a*b*4T1*T3
R12=
	x*z

	a		x
Δ1∼Δ3⇔		=		⇔a*b=x*z⇔
	z		b

R₁²=4T₁*T₃

5-latek: Dobry wieczor Na razie CI bardzo dziekuje . Musze to rozpracowac sobie . Mam pytanie do tego Dlaczego bierzemy pola do potegi drugiej ?

Mila: Aby uniknąć pierwiastków .

5-latek: Dobrze No to dalej R₃= e*f*sinγ Do niego przystaja trojkaty nr 1 i nr 2

	2T1
T1=0,5* z*f*sinγ⇒sinγ=
	z*f

	2T2
T2= 0,5*e*y*sinγ⇒sinγ=
	e*y

	e*f*4T1*T2
R32= e2*f2*sin2γ=
	z*y

	z		e
Trojkaty nr 1 i nr 2 sa podobne na posdatwie cechy KKK wiec		=		⇒z*y= e*f
	f		y

wiec r₃²= 4T₁*T₂ R₂= c*d*sinβ Do niego sa przylegle trojkaty nr 2 i nr 3

	2T1
T2= 0,5*c*y*sinβ⇒sinβ=
	c*y

	2T3
T3= 0,5*x*d*sinβ⇒sinβ=
	x*d

	c*d
R22= c2*d2*sin2β=		{y*x}
	4T2*T3

	c
Trojkaty nr 2 i nr3 sa podobne na podsatwie cechy KKK wiec z tego mamy		= x}{d} ⇒c*d=
	y

y*x R₂²= 4T₂*t₃ Mamy tak {R₁²= 4T₁*T₃ {R₂²= 4*T₂*T₃ {R₃²= 4*T₁*T₂ I dalej sie zatrzymalem

Mila:

R12		T1
	=
R22		T2

	R12
T1=		*T2
	R22

	R12
R32=4*		*T2*T2
	R22

	R22
T22=R32*
	4R12

	R3*R2
T2=
	2R1

5-latek: Dzien dobry Milu Dziekuje . zaraz to sobie przeanalizuje

Mila: