krótki opis zadania RoZsTrOjOnY: Geometria − mój odwieczny nemesis... Czworokąt ABCD jest opisany na okręgu o środku O. Wiadomo, że OA=OC=1 oraz OB=OD=2. Obliczyć obwód tego czworokąta. Wiem, ze szukanym czworokątem jest rąb, a rozwiązaniem 4√5, ale nie wiem jak ładnie udowodnić jego "rąbowatość"

RoZsTrOjOnY: up

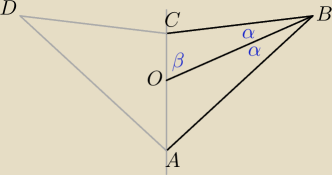
g: Załóż że OB=OD, ale punkty B,O,D nie leżą na jednej prostej. Wówczas nie mogło by być OA=OC.

OC		CB
	=
sinα		sinβ

OA		AB		AB
	=		=
sinα		sin(180−β)		sinβ

OC		CB
	=		> 1
OA		AB

RoZsTrOjOnY: q, jesteś moim matematycznym bogiem <3