aa PrzyszlyMakler:

	1
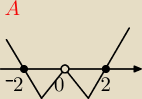
Wyznacz przedziały monotoniczności funkcji f(x) = x +		a następnie rozstrzygnij w
	x

którym punkcie x₁ = log₇4 czy x₂= log₇3 funkcja przyjmuje większą wartość? Mam pytanie: bo

	x2+1
f(x) =
	x

	2x*x−(x2+1)
f'(x)=
	x2

	x2−1
f'(x)=
	x2

D: x ∊ℛ − {−2,2} rozstrzygnij w którym punkcie x₁ = log₇4 czy x₂= log₇3 funkcja przyjmuje większą wartość x₁> x₂ i jak rozstrzygnąć czy są to liczby z przedziału (1;2) czy (2;+niesk) bez kalkulatora naukowego?

Jerzy: A do czego Ci pochodna dla rozstrzygnięcia tej kwestii ?

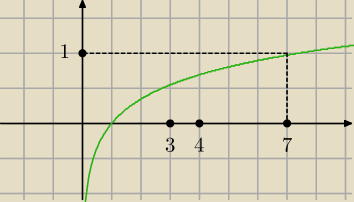
Jerzy: Chyba już wiem o co Ci chodzi.... pomogło ?

PrzyszlyMakler: Nie. Ja rozumiem, że log₇4 > log₇3 ALE moja funkcja rośnie dla x>2 i maleje dla x<2 więc aby ustalić dla którego arguemtnu przyjmie ona większą wartośc to muszę oszacować, czy liczba log₇4 jest liczbą z zakresu (0;2) czy liczbą z zakresu (2;+niesk) bo to zmienia czy moja funkcja na tym argumencie rośnie czy maleje a w efekcie czego czy dla argumentu większego czy mniejszego przyjmie większoą wartość

Jerzy: Na rysunku, który pokazałem widać ,że obie te liczby należą do przedziału (0,1)

PrzyszlyMakler: A OK. Sorry, chyba nie myśle Dziękuję