Oblicz pole obszaru D ograniczonego krzywymi Studentka : Oblicz pole obszaru D ograniczonego krzywymi y=sinx y=cos2x x=0 dla x≥0

Jerzy: Tylko takie ograniczenia ?

Studentka : tak

Jerzy: To wychodzi suma nieskończenie wielu obszarów

Studentka : wiem, czyli nie da się rozwiązać?

Jerzy: Wg mnie powinno być jeszcze jedno ograniczenie ...masz odpowiedź ?

Studentka : nie mam :<

Studentka : ∫√(4=x)/(4−x)dx potrafisz zrobić za to dobre podstawienie?

Studentka : chyba już mam

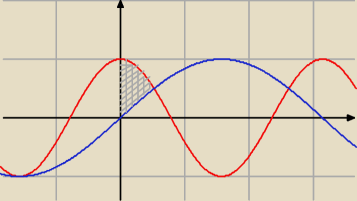
yht: Obszar normalny względem osi x bo jest jeden rodzaj linii ograniczającej z góry (czerwona) i jeden rodzaj ograniczenia z dołu (niebieska linia) granice całkowania dla x 0 ≤ x ≤ ? górną granicę całkowania dla x obliczę, rozwiązując równanie sin(x) = cos(2x) i biorąc

	π
rozwiązanie dodatnie, dla 1 ćwiartki czyli x∊(0,		)
	2

sin(x) = cos(2x) sin(x) = cos²(x) − sin²(x) sin(x) = 1−sin²(x) − sin²(x) 2sin²(x) + sin(x) − 1 = 0 sin(x) = t, t∊<−1,1> 2t² + t − 1 = 0 Δ = 1−4*2*(−1) = 1+8 = 9 √Δ = 3

	−1−3		−4
t1 =		=		= −1
	2*2		4

	−1+3		1
t2 =		=
	2*2		2

	1
sin(x) = −1 lub sin(x) =
	2

	π		π		5π
x = −		+ 2kπ, lub x =		+2kπ lub x=		+2kπ, k − całkowite
	2		6		6

	π		π
warunek x∊(0,		) spełnia tylko x =
	2		6

czyli granice całkowania dla x to

	π
0 ≤ x ≤
	6

z góry obszar ograniczony jest przez f₂(x) = cos(2x) a z dołu przez f₁(x) = sin(x) P = ∫₀^π/6 f₂(x) − f₁(x) dx = ∫₀^π/6 cos(2x) − sin(x) dx =

	1
=		sin(2x) + cos(x) |π/60 =
	2

	1		1
=		sin(2*π/6)+cos(π/6) −		sin(2*0)−cos(0) =
	2		2

	1		1
=		sin(π/3)+cos(π/6) −		sin(0)−cos(0) =
	2		2

	1		√3		√3		1
=		*		+		−		*0−1 =
	2		2		2		2

	√3		√3		3√3		3√3−4
=		+		− 1 =		− 1 =
	4		2		4		4

https://www.wolframalpha.com/input/?i=area+between+y%3Dcos(2x),+y%3Dsin(x)+from+x%3D0+to+x%3Dpi%2F6

Studentka : dziękuję baaardzo