Obliczyć pole obszaru D ograniczonego krzywymi Studentka : x² +y² −4x −2y +4=0 y=x y=0

Jerzy:

	1
P =		π
	4

...zrób sobie rysunek

Jerzy: Nie .... źle

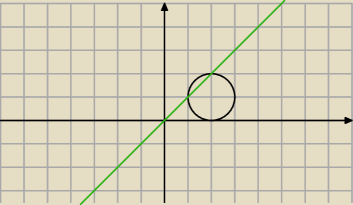
Jerzy: Tutaj masz dobry rysunek ... ustal granice całkowania.

Studentka : od 1 do 3, ale nie wiem jak wyłuskać z tego y, żeby podstawić do wzoru

Jerzy: Popatrz uważnie na rysunek, jaki to obszar.

Studentka : okrąg

Jerzy: Masz odpowiedź do tego zadania ?

Studentka : niestety nie, jutro mam za to z tego egzamin :<

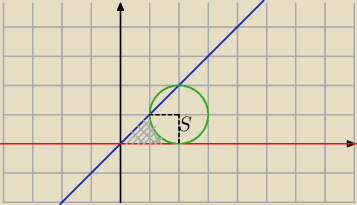
yht: x²+y²−4x−2y+4=0 x²−4x+y²−2y+4=0 x²−4x+4−4+y²−2x+1−1+4=0 (x−2)²−4+(y−1)²−1+4=0 (x−2)²+(y−1)²=1 S=(2,1), r=1 Pole szukanego (szarego) obszaru P_S policzymy, odejmując od pola trapezu P_t (w którym a=2, b=1, h=1) pole ćwiartki koła P_ć o promieniu r = 1 P_S = P_t − P_ć

	(a+b)*h		(2+1)*1		3
Pt =		=		=
	2		2		2

	1		1		π
Pć =		* πr2 =		*π*12 =
	4		4		4

	3		π
PS =		−
	2		4

Obyło się bez całki

Studentka : dziękuję!