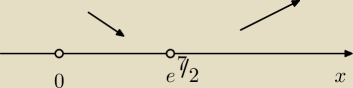
Zbadać monotoniczność i ekstremum funkcji. pytanie: Zbadać monotoniczność i ekstremum funkcji. g(x) = ln²x −7lnx + 4 D=(0,+oo) g'(x) = 2lnx −7 / x g(x) = 0 <=> 2lnx−7 / x = 0 = > 2lnx −7 = 0 => x = e^7₂ I teraz proszę o sprawdzenie czy poprawnie badam znak pochodnej funkcji. g'(x) > 0 <=> 2lnx−7 > 0 => x > e^7₂ g'(x) < 0 <=> 2ln − 7 < 0 => x < e^7₂ Funkcja g(x) maleje na przedziale (0, e^7₂) Funkcja g(x) rośnie na przedziale (e^7₂, +oo) Pochodna ujemna na przedziale (0, e^7₂) Pochodna dodatnia na przedziale (e^7₂, +oo) Pochodna zmienia znak z ujemnego na dodatni, wiec w punkcie e^7₂ jest minimum lokalne. L I teraz pytanie czy takie coś wystarczy wykładowcy do zaliczenia tego zadania? I mam jeszcze jedno pytanie czy można zbadać znak pochodnej w inny sposób?

pytanie: @ UP

pytanie: @ UP x2