| 1 | ||
a podstawowy okres tej funkcji jest równy | π. | |
| 4 |
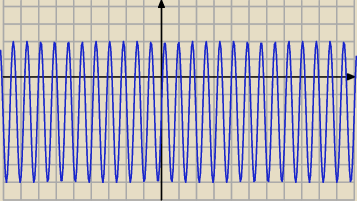 c = 8
− 1 ≤ sin cx ≤ 1 / * b
− b ≤ b sin cx ≤ b ? + a
a − b ≤ a + b sin cx ≤ a + b
a − b = − 6 a + b = 2
więc
2 a = − 4 ⇒ a = − 2
b = 2 − a = 2 − (−2) = 4
Odp. a = − 2, b = 4 , c = 8
f(x) = − 2 + 4 sin ( 8 x)
c = 8
− 1 ≤ sin cx ≤ 1 / * b
− b ≤ b sin cx ≤ b ? + a
a − b ≤ a + b sin cx ≤ a + b
a − b = − 6 a + b = 2
więc
2 a = − 4 ⇒ a = − 2
b = 2 − a = 2 − (−2) = 4
Odp. a = − 2, b = 4 , c = 8
f(x) = − 2 + 4 sin ( 8 x)
| 2π | ||
T= | − okres funkcji y=sin(cx) | |
| c |
| 2π | π | ||
= | ⇔ | ||
| c | 4 |
| |−6−2| | ||
−1≤sin(8x)≤1 /*4 ponieważ | =4 długość przedziału podzielona na 2 | |
| 2 |
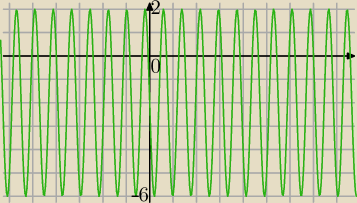 I drugie rozwiązanie .
c=8 jak wcześniej
8 jednostek − długość przedziału zbioru wartości.
−1≤sin(8x)≤1 /*−4
4≥−4sin(8x)≥−4 /−2
2≥−2−4sin(8x)≥−6⇔
−6≤−2−4sin(8x)≤2
a=−2
b=−4
c=8
f(x)=−2−4sin(8x)
I drugie rozwiązanie .
c=8 jak wcześniej
8 jednostek − długość przedziału zbioru wartości.
−1≤sin(8x)≤1 /*−4
4≥−4sin(8x)≥−4 /−2
2≥−2−4sin(8x)≥−6⇔
−6≤−2−4sin(8x)≤2
a=−2
b=−4
c=8
f(x)=−2−4sin(8x)