wyznacz przedziały monitonicznośc i ekstrema lokalne funkcji matura: y= x⁴−2x³−3 f. malejąca x= ( −≈,0)i (0,3/2) f. rosnąca (3/2, ≈) funkcja posiada minimu lokalne dla x= 3/2 dobrze, cyz gdzies namieszalam?

zef: Wygląda ok

matura: bo nie wiem czy sobie dobrze narysowalam falke pomocnicza i cos mi sie tu nie podoba

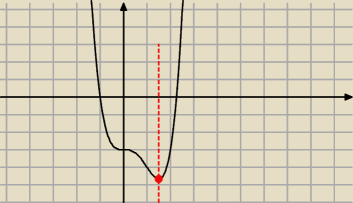
zef: y=x⁴−2x³−3 y'=4x³−6x²= x²(4x−6) Wykres funkcji y=x⁴−2x³−3

matura: a tutaj w tym wypadku y= x²(x−1)² f. malejąca = (0,1) f. rosnąca (≈,0) i (1,≈) x=0 maksimum lokalne x=1 minimum lokalne

zef: DfeR, Df'eR y=x²(x²−2x+1)=x⁴−2x³+x² y'=4x³−6x²+2x y'=0 ⇔ 4x³−6x²+2x=0 , x(4x²−6x+2)=0 x=0 lub 4x²−6x+2=0 Δ=36−32

	6−2
x1=		=0,5
	8

	6+2
x2=		=1
	8

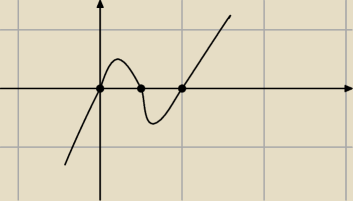
y'=4x(x−1)(x−0,5) f maleje dla x∊(−∞;0),(0,5;1) f rośnie dla x∊(0;0,5),(1;∞) maksimum w 0,5 minimum w 0 i 1

matura: dziekowac

matura: a z tym przykladem pomozesz? y= x²(4−x²)³ tyle mi wyszla pochodna : 8x(16−24x²+9x⁴+x⁶) i teraz nie wiem jak dalej to sobie rozpisac bo jakies brednie mi wychodza..

zef: pochodna to 8x(16−24x²+9x⁴−x⁶) 8x=0 lub 16−24x²+9x⁴−x⁶=0 dajmy podstawienie x²=t może tak będzie ci łatwiej