Ustawienia ludzi przy stole tajemniczyczlowiek: Przy okrągłym stole posadzono losowo 4 osoby. Wśród nich są osoby A i B. Oblicz p−podobieństwo zdarzenia, że: a) Osoby A i B siedzą obok siebie b) osoby A i B siedzą naprzeciwko Mam problem z Ω, bo nie wiem czy dobrze myślę: Ω=4! co do a) wydaje mi się że moc zdarzenia A to 2*2!

Jerzy: Jeśli krzesła ( miejsca ) nie są numerowane , to: |Ω| = 4!

tajemniczyczlowiek: Z odpowiedzi wynika że P(A) = 2/3 a P(B) = 1/3, więc 4! nie pasuje, czyli trzeba jakoś inaczej policzyć Ω

Jerzy: Moja pomyłka... |Ω| = 3!

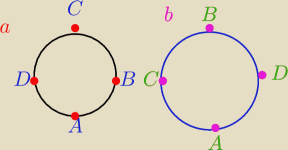
XP: Krzesła jednakowe.

	4!
|Ω|=		=3! =6 dzielimy przez 4 ponieważ obrót o 45o nie zmienia sąsiadów
	4

a) A− (A i B) siedzą obok siebie (A,B) − traktujemy jako jeden element, mamy do ustawienia 3 elementy

	2*3!
|A|=		=2*2=4
	3

	4		2
P(A)=		=
	6		3

b) B− A i B siedzą naprzeciw siebie

	3!
|B|=		=2
	3

Zmiana miejsc między A i B uwzględniona w pewnej permutacji.

	2		1
P(B)=		=
	6		3

To chyba wg intencji autora zadania.

tajemniczyczlowiek: Dziękuję XP za pomoc