Geometrii troszkę ( ͡° ͜ʖ ͡°): Czworokąt ABCD jest wpisany w okrąg, przy czym styczne do tego okręgu w punktach B i D przecinają się na prostej AC. Wykaż, że AB*CD=AD*BC rysunek: https://scr.hu/GeK6zM

( ͡° ͜ʖ ͡°): byłby ktokolwiek w stanie mnie chociaz naprowadzić na rozwiązanie?

( ͡° ͜ʖ ͡°): <bump>

( ͡° ͜ʖ ͡°): <bump>

( ͡° ͜ʖ ͡°): <ostatnia próba podbicia wątku :c>

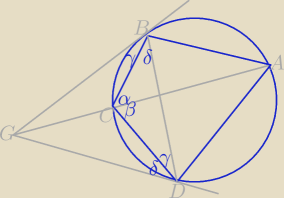
Rafal: Równości kątów na rysunku wynikają z twierdzenia o kącie między styczną i cięciwą.

	GB		GC
Z twierdzenia sinusów		=		, a ponieważ sin(180−α)=sinα, to
	sin(180−α)		sinγ

	GB		sinα
		=		.
	GC		sinγ

	GD		sinβ
Podobnie dowodzimy, że		=		.
	GC		sinδ

	sinα		sinβ
Z równości odcinków stycznych		=		.
	sinγ		sinδ

	AB		sinα		AD		sinβ
Znów z twierdzenia sinusów		=		oraz		=		, a wobec
	BC		sinγ		CD		sinδ

	AB		AD
wcześniejszych równości		=		. Przekształcamy tę równość i do widzenia.
	BC		CD

( ͡° ͜ʖ ͡°): Dzięki wieeeelkie