ttt tade: Zerknie ktoś? wyszedł mi zły wynik, po prawie godzinie pisania doszedłem do takiego wyniku jak w odpowiedzi tylko zamiast minusa u mnie jest plus

	1		sinαsinβ		2sinαcosβ
Prawidłowa odp to		πc3		(1−		)
	3		sin(α+β)		sin(α+β)

Treść: w trójkacie abc dane są AB=c kąt CAB = α kąt ABC = β oblicz objetosc bryły powstalej z obrotu trojkąta ABC wkół prostej zawierającej bok AC Zdjecie: http://imgur.com/a/Qk551 Prosze o pomoc bo juz niemam siły drugi raz tego przepisywać

tade: help

Mila: Zaraz.

Mila: Chyba inna treść tego zadania. Tam w rozwiązaniu masz inny obrót.

tade: źle przepisałem trójkąt obraca się wokól prostej zawierajacej wysokosc opuszczona z wierzchołka C, Mila zerkniesz jeszcze raz jesli możesz?

Mila: Już patrzę.

Mila: i kąt β>90 , tak?

tade: tak β>90

Mila:

	1		1
V=		π*R2*H−		π*r2*H=
	3		3

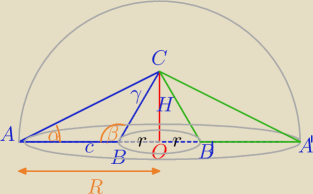
	1		1
=		π*H*(R2−r2)=		π*H*(R−r)*(R+r)
	3		3

	1
V=		π*H*c*(c+2r)
	3

γ=180−(α+β)

AC		BC		c
	=		=
sinβ		sinα		sin(α+β)

	c*sinα
|BC|=
	sin(α+β)

W ΔCOB:

	H		c*sinα*sinβ
sin(180−β)=		⇔H=
	|BC|		sin(α+β)

================================

	r		c*sinα*(−cosβ)
cos(180−β)=		⇔r=		i tu mamy różnicę, β>90o
	BC		sin(α+β)

cosβ<0 natomiast cos(180−β)>0

	1		c*sinα*sinβ		2c*sinα*(−cosβ)
V=		*π*		*c*[c−		]
	3		sin(α+β)		sin(α+β)

	1		c3*sinα*sinβ		2sinα*sinβ
V=		π*		*[1−		]
	3		sin(α+β)		sin(α+β)

==================================

tade: Dziekuje

Mila: