Pole ograniczone krzywymi
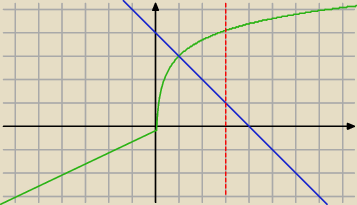
Johny : Y=3+lnx
Y=4−x
X=e
26 sty 10:05
Jerzy:
26 sty 10:09
Johny : A jak pole policzyć ? Proszę po kolei
26 sty 10:12
Jerzy:
P = a∫b(lnx+3)dx + b∫c(4−x)dx
a = e−3
b= 1
c = 4 − e
26 sty 10:18
qqqqqqqqqqqqqw: calke po jednym drugim i trzecim
26 sty 10:18
Jerzy:
Wróć ... podałem złe granice całkowania.
26 sty 10:20
Jerzy:
No i całka będzie inna... zaraz napiszę.
26 sty 10:21
Jerzy:
P = 1∫4−e (lnx + 3 + 4 − x)dx
26 sty 10:22
Jerzy:
Jeszcze drobny bład .... ∫(lnx + 3 + x − 4) dx
26 sty 10:25
Johny : Obliczylbys mi to ?
26 sty 10:28
Jerzy:
A na kolokwium też pójdę za Ciebie ?

26 sty 10:28
Jerzy:
∫(lnx + x − 1)dx = ∫lnxdx + ∫xdx −∫dx .... i popracuj teraz trochę sam.
26 sty 10:29
Johny : Wejście jestem i nie daje rady
26 sty 10:30
Jerzy:
Potrafisz policzyć ∫lnxdx ( przez części )
26 sty 10:31
Johny : Proszę rozkosz wszystko po kolei
26 sty 10:36
Johny : Rozpisz*
26 sty 10:38
Jerzy:
| | 1 | |
P = [ x(lnx − 1) + |
| x2 − x ] ..... i podstawiaj granice całkowania. |
| | 2 | |
26 sty 10:49

