Oblicz (-√3+i)^7 Darek: Oblicz (−√3+i)⁷ . Wynik podaj w postaci algebraicznej

Janek191: ( − √3 + i )⁷ = [( −√3 + i)²]² *( −√3 + i)²*( −√3 + i) = = ( 3 − 2√3 i − 1)²*( 2 − 2 √3 i)*( −√3 + i) = = 2²*( 1 − √3 i)²* 2*( 1 − √3 i)*( − √3 + i) = = 8*( 1 − 2√3i − 3)*( −√3 + i + 3 i + √3) =8*(−2)*( √3 i + 1)(4 i) = = − 64*(− √3 + i ) = 64 √3 − 64 i Jak się nie pomyliłem. II sposób − √3 + i zapisz w postaci trygonometrycznej i zastosuj wzór Moivre'a

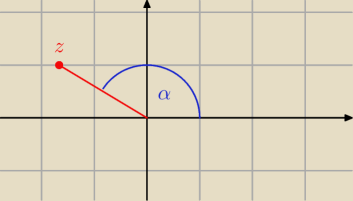
Janek191: z = − √3 + i I z I = 2

	−√3		1
cos α =		sin α =
	2		2

	π		π		5
α =		+		=		π
	2		3		6

	5		5		5		5
Z7 = 27*( cos (7*		π + i sin ( 7*		π) = 128*(cos 5		π + i sin 5		π) =
	6		6		6		6

	5		5		5		5
= 128*( cos ( π +		π + i sin ( π +		π) = 128*( − cos		π − i sin		π) =
	6		6		6		6

	√3		1
= 128*(		− i *		) = 64*( √3 − i) = 64 √3 − 64 i
	2		2