romb. melania.: i mam jeszcze jedno zadanko, i nie umiem go zrobic. stosunek dlugosci przekatnych rombu wynosi 3:4. oblicz stosunek pola rombu do pola kola wpisanego w ten romb. prosze o pomoc.

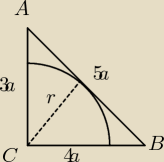
tom: na rysunku jest "ćwiartka" rombu, połowy przekątnych to odpowiednio 3a i 4a więc bok rombu wynosi 5a( tw. Pitagorasa, przy okazji to tzw. złoty Δ o bokach 3,4,5). Wysokość ΔABC jest promieniem okręgu wpisanego w romb. Jego długość można wyliczyć np. z wzorów na pole Δ

	12
5a*r=3a*4a ⇒r=		*a.Pole koła wpisanego πr2, pole rombu 3a*4a............
	5

melania.: dzieki.